题目内容
如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过CA1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段CA1,A1C1,C1A2,…,则第10条线段A5C5= .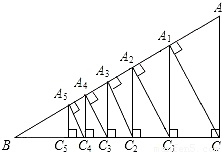
【答案】分析:根据角的正弦函数与三角形边的关系,可求出各边的长,然后再总结出规律.
解答:解:根据勾股定理,得AB=5,
则sinA= .
.
∴A1C=3× .
.
在直角三角形A1C1C中,
根据锐角三角函数得
A1C1=3×( )2
)2
以此类推,则A5C5=3×( )10.
)10.
点评:此题主要考查运用锐角三角函数定义表示未知的边及分析归纳能力.
解答:解:根据勾股定理,得AB=5,
则sinA=
 .
.∴A1C=3×
 .
.在直角三角形A1C1C中,
根据锐角三角函数得
A1C1=3×(
 )2
)2以此类推,则A5C5=3×(
 )10.
)10.点评:此题主要考查运用锐角三角函数定义表示未知的边及分析归纳能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
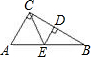 如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
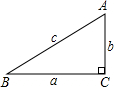 如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )
如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y=
(2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y= 如图,已知直角三角形ABC的周长为
如图,已知直角三角形ABC的周长为