题目内容
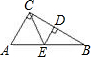 如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
分析:根据CE=EB得∠B=∠BCE,所以∠A=∠ACE,得AE=CE=EB.所以A、B都正确;
因为∠ACB=90°,ED⊥CB,所以AC∥ED.则∠A=∠DEB,∠CED=∠ACE.又∠A=∠ACE,所以∠CEB=2∠A.故C正确;
当∠B=30°时,D才成立.
因为∠ACB=90°,ED⊥CB,所以AC∥ED.则∠A=∠DEB,∠CED=∠ACE.又∠A=∠ACE,所以∠CEB=2∠A.故C正确;
当∠B=30°时,D才成立.
解答:解:∵CE=EB,∴∠B=∠BCE.
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,∠A+∠B=90°.
∴∠A=∠ACE.
∴AE=CE=EB.
故选项A、B都正确;
∵∠ACB=90°,ED⊥CB,
∴AC∥ED.
则∠A=∠DEB,∠CED=∠ACE.
又∠A=∠ACE,
∴∠CEB=2∠A.
故选项C正确;
当∠B=30°或∠A=60°时,选项D才成立.
故选D.
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,∠A+∠B=90°.
∴∠A=∠ACE.
∴AE=CE=EB.
故选项A、B都正确;
∵∠ACB=90°,ED⊥CB,
∴AC∥ED.
则∠A=∠DEB,∠CED=∠ACE.
又∠A=∠ACE,
∴∠CEB=2∠A.
故选项C正确;
当∠B=30°或∠A=60°时,选项D才成立.
故选D.
点评:此题主要考查了等腰三角形的性质和判定、平行线的判定和性质等知识点,难度不大.

练习册系列答案
相关题目
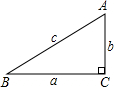 如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )
如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y=
(2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y= 如图,已知直角三角形ABC的周长为
如图,已知直角三角形ABC的周长为