Question

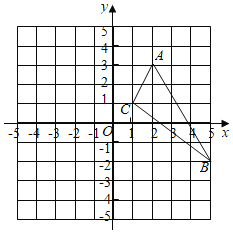
【题目】对于平面直角坐标系 xOy 中的点 A，给出如下定义：若存在点 B（不与点 A 重合，且直线 AB 不与 坐标轴平行或重合），过点 A 作直线 m∥x 轴，过点 B 作直线 n∥y 轴，直线 m，n 相交于点 C．当线段 AC，BC 的长度相等时，称点 B 为点 A 的等距点，称三角形 ABC 的面积为点 A 的等距面积． 例如：如 图，点 A（2，1），点 B（5，4），因为 AC= BC=3，所以 B 为点 A 的等距点，此时点 A 的等距面积为．

(1)点 A 的坐标是（0，1），在点 B1（2，3），B2 (1， 1) ， B3 (3， 2) 中，点A的等距点为 ．

(2)点 A 的坐标是 (3，1) ，点 A 的等距点 B 在第三象限，

①若点 B 的坐标是 (5， 1) ，求此时点 A 的等距面积；

②若点 A 的等距面积不小于 2，请直接写出点 B 的横坐标 t 的取值范围．

Answer 1

【答案】（1）B1，B3；（2）①2；②t≤-5或-1≤t＜0

【解析】

（1）根据等距点的定义可作判断；

（2）①计算等腰直角△ACB的面积即可；

②根据题意画出全等的等腰直角三角形ABC和AB1C1，发现点B可以在射线BF上或线段B1M上，可得t的取值．

解：（1）如图1，过A作x轴的平行线m，过B1作y轴的平行线n，交于C1，

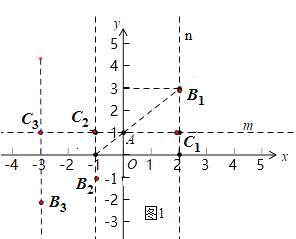
∵点A的坐标是(0，1)，在点B1(2，3)，

∴AC1=B1C1=2，即B1是点A的等距点，

同理：AC3=B3C3=3，B3是点A的等距点，

AC2≠B2C2，B2不是点A的等距点，

故答案为B1，B3；

（2）①如图2，根据题意，可知AC⊥BC．

∵A(-3，1)，B(-5，-1)，

∴AC=BC=2．

∴三角形ABC的面积为：ACBC==2．

∴点A的等距面积为2．

②∵三角形ABC的面积为：ACBC≥2，

∴AC=BC≥2，

如图3，根据①作全等的等腰直角三角形ABC和AB1C1，发现点B可以在射线BF上或线段B1M上，

∵A(-3，1)，

∴B(-5，-1)，B1(-1，-1)，

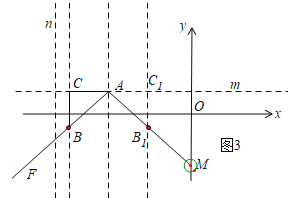
∴点B的横坐标t的取值范围是t≤-5或-1≤t＜0．