题目内容
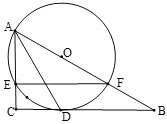
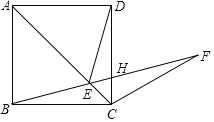
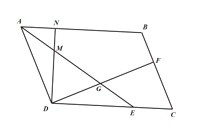
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
【答案】(1)见解析;(2)AB =a+b;(3)![]()
【解析】
(1)AE是∠BAD的角平分线 ,则∠BAE=∠DAE,四边形ABCD是平行四边形,则AB∥CD ,∠BAD=∠C,求得∠ADN=∠CDF,由AB∥CD知∠BAE=∠DEA,所以∠DAE=∠DEA,所以AD=DE.根据ASA证明△ADM≌△EDG,所以AM=EG.
(2) 过点A作HA⊥AD交DN的延长线于H,证明△DHA≌△DCF(ASA) , CF=AH=b DH=DC=AB.通过∠AMH=∠HAM,知HM=AH=CF=b .通过前面的全等知DM=DG =a,求得HD的长度.故知AB的长度.
(3) AB∥DC知对应线段成比例,由此可知![]() =
=![]() =
=![]() ,易得DN=
,易得DN=![]() , DA=DE 即AD=3AN, 在Rt△AND中,根据勾股定理可知
, DA=DE 即AD=3AN, 在Rt△AND中,根据勾股定理可知![]() , 由△ADN∽△CDF可知对应边成比例,可求得DC的长度,继而求得CE的长度.
, 由△ADN∽△CDF可知对应边成比例,可求得DC的长度,继而求得CE的长度.
(1)证明:∵AE是∠BAD的平分线
∴ ∠BAE=∠DAE
∵DN⊥DC 、DF⊥BC
∴ ∠NDA=90° ∠DFC=90°
∵四边形ABCD是平行四边形
∴AB∥CD ∠BAD=∠C
∴∠DAE=∠DEA ∠ADN=∠EDG
∴ DA=DE
∴ △ADM≌△EDG(ASA)
∴AM=EG
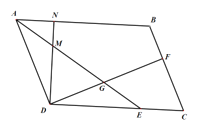
(2)如图,过点A作HA⊥AD交DN的延长线于H.
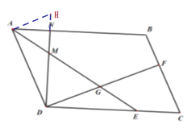
∴∠HAD=∠DFC=90°
∵∠ADH=∠FDC AD=DF
∴ △DHA≌△DCF(ASA)
∴CF=AH=b DH=DC=AB
易证 ∠AMH=∠HAM
∴HM=AH=CF=b
∵△ADM≌△EDG(已证)
∴DM=DG =a
∴AB=DC=DM+MH =a+b
(3) CE =DC-DE=![]() -2.
-2.
理由如下:
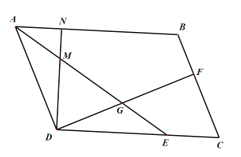
在□ABCD中,AB∥DC
∴![]() =
=![]() =
=![]() ,
,
∵ ![]() =
=![]() ∴
∴![]() =
=![]() =
=![]() ,
,
∵DG=DM=![]() ∴MN=
∴MN=![]() , 即
, 即![]()
∵ DA=DE 即AD=3AN,
∴在Rt△ADN中,![]()
![]()
易证:△ADN∽△CDF
∴![]()
即 ![]() =
=![]()
∴![]()
∴CE =DC-DE= ![]()

【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
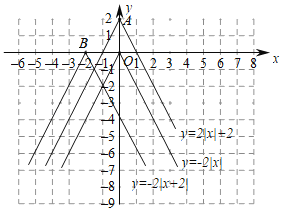
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
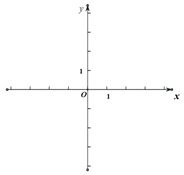
(3)拓展应用:在所给的平面直角坐标系内画出函数的图象.若点
![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.