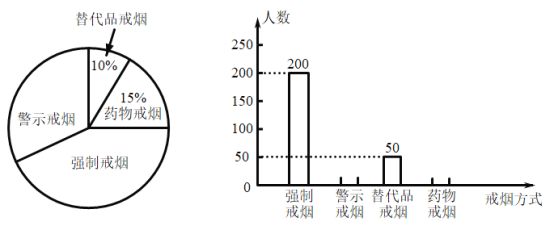
��Ŀ����
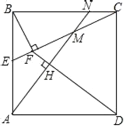
����Ŀ����ͼ1����һ����ĺ����ϰѣ�ͼ2����ƽ��ʾ��ͼ��EH���ϰѰ��֣�F�ǰ��ֵ�һ���̶��㣬���లװ����Ƭ��Ǽ�PA��PB�ϣ��ǼܵĶ˵�Pֻ�����߶�FH���ƶ�����������ȫ�ſ�ʱ��PA��PB�ֱ���HMHN�غϣ�������պ�ʱ��PA��PB��FH�غϣ���ֱ֪��EH=120cm��FH=20cm��
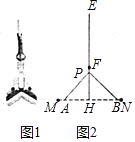
(1)����APB=90������EP�ij�(�����������)
(2)����APB=26������MA�ij�(�������С�����һλ)
(3)�������ȫ�ſ����պϵĹ����У�ֱ��д��PA���е�Q�˶���·������(�ο����ݣ�sin13���0.225��cos13���0.974��tan13���0.231����ȡ3.14)
���𰸡�(1)(120��10![]() )cm��(2)15.5(cm)��(3)15.7(cm)
)cm��(2)15.5(cm)��(3)15.7(cm)
��������
(1)��������ȫ�ſ�ʱ��PA��PB�ֱ���HMHN�غϣ�������պ�ʱ��PA��PB��FH�غϣ��ó�PA=PB=FH=HM=HN=20��֤����APB�ǵ���ֱ�������Σ�������֪��EH��MN���ó���APHҲ�ǵ���ֱ�������Σ��ɵ���ֱ�������ε����ʵó�PA=![]() PH���ó�PH=
PH���ó�PH=![]() PA=
PA=![]() �����ɵó��𰸣�
�����ɵó��𰸣�
(2)�ɵ��������ε����ʵó���APH=��BPH���ó���APH=![]() ��APB=
��APB=![]() =13����AH=PAsin13���20��0.225=4.5�����ɵó��𰸣�
=13����AH=PAsin13���20��0.225=4.5�����ɵó��𰸣�
(3)��ֱ��������б���ϵ��������ʵó�HQʼ�յ���![]() PA=10cm���ó�Q�˶��Ĺ켣����HΪԲ�ģ��뾶Ϊ10cm��90��Բ�����ɻ�����ʽ���ɵó��𰸣�
PA=10cm���ó�Q�˶��Ĺ켣����HΪԲ�ģ��뾶Ϊ10cm��90��Բ�����ɻ�����ʽ���ɵó��𰸣�
(1)�ߵ�������ȫ�ſ�ʱ��PA��PB�ֱ���HMHN�غϣ�
������պ�ʱ��PA��PB��FH�غϣ�
��PA=PB=FH=HM=HN=20��
�ߡ�APB=90����
���APB�ǵ���ֱ�������Σ�
������֪��EH��MN��
���APHҲ�ǵ���ֱ�������Σ�
��PA=![]() PH��
PH��
��PH=![]() PA=
PA=![]() ��20=10
��20=10![]() ��
��
��EP=EH��PH=(120��10![]() )cm��
)cm��
(2)��PA=PB��EH��MN��
���APH=��BPH��
���APH=![]() ��APB=
��APB=![]() ��26��=13����
��26��=13����
AH=PAsin13���20��0.225=4.5��
��MA=HM��AH=20��4.5=15.5(cm)��
(3)��EH��MN��Q��PA���е㣬
��HQʼ�յ���![]() PA=10cm��
PA=10cm��
��Q�˶��Ĺ켣����HΪԲ�ģ��뾶Ϊ10cm��90��Բ����
���Q�˶���·����=![]() ��
��![]() =15.7(cm)
=15.7(cm)

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�