题目内容
(1)如图,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC.
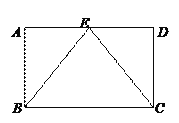
(2)如图,AB与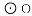

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
题目内容
(1)如图,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC.

(2)如图,AB与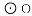
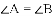

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案