Question

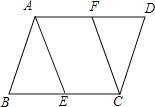
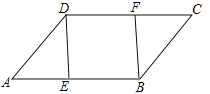
【题目】如图，在ABCD中，E、F分别是AB、DC边上的点，且AE=CF，

（1）求证：△ADE≌△CBF；

（2）若∠DEB=90°，求证：四边形DEBF是矩形．

Answer 1

【答案】（1）证明见试题解析；（2）证明见试题解析．

【解析】

试题分析：（1）在ABCD中，AE=CF，可利用SAS判定△ADE≌△CBF；

（2）在ABCD中，且AE=CF，利用一组对边平行且相等的四边形是平行四边形，可证得四边形DEBF是平行四边形，又由∠DEB=90°，可证得四边形DEBF是矩形．

试题解析：（1）∵四边形ABCD是平行四边形，∴AD=CB，∠A=∠C，在△ADE和△CBF中，∵AD=CB，∠A=∠C，AE=CF，∴△ADE≌△CBF（SAS）；

（2）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∵AE=CF，∴BE=DF，∴四边形ABCD是平行四边形，∵∠DEB=90°，∴四边形DEBF是矩形．