题目内容
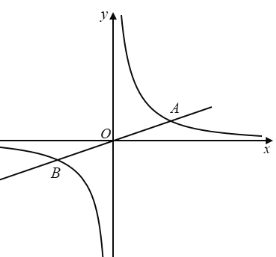
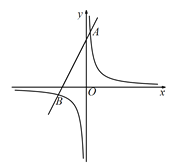
【题目】抛物线y=x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C.
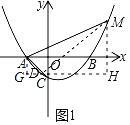
(1)如图1,若OB=2OA=2OC
①求抛物线的解析式;
②若M是第一象限抛物线上一点,若cos∠MAC=![]() ,求M点坐标.
,求M点坐标.
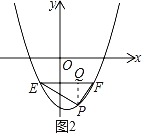
(2)如图2,直线EF∥x轴与抛物线相交于E、F两点,P为EF下方抛物线上一点,且P(m,﹣2).若∠EPF=90°,则EF所在直线的纵坐标是否为定值,请说明理由.
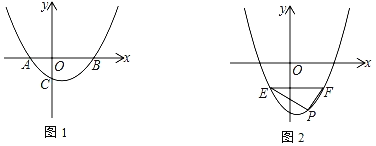
【答案】(1)①y=x2-![]() x-
x-![]() ;②M坐标为(
;②M坐标为(![]() ,
,![]() );(2)EF所在直线的纵坐标是定值,理由见解析.
);(2)EF所在直线的纵坐标是定值,理由见解析.
【解析】
(1)①由x=0得到点C坐标为(0,c),故可以用c表示OA、OB进而表示点A、B坐标,把含c的坐标代入抛物线解析式即求得b、c的值;
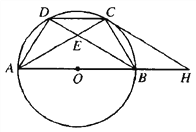
②过点M作MD⊥AC于点D,得出cos∠MAC=![]() ,进而MD=4AD.在MD、AD下方构造等腰直角△MDH和△ADG,则相似比为4.设AD=DG=t,用t表示DH和MH,进而用t表示点M坐标,代入抛物线解析式即求得t的值;
,进而MD=4AD.在MD、AD下方构造等腰直角△MDH和△ADG,则相似比为4.设AD=DG=t,用t表示DH和MH,进而用t表示点M坐标,代入抛物线解析式即求得t的值;
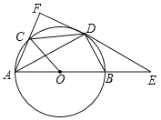
(2) 由点P(m,-2)在抛物线上得c+2=-m2-bm.设点E、F纵坐标为n,代入抛物线解析式根据韦达定理得xE+xF=-b,xExF=c-n.过点P作PQ⊥EF于点Q,易证△EPQ∽△PFQ,进而得PQ2=EQFQ,用含n、m、xE、xF的式子表示PQ、EQ、FQ解得n=-1,故点E、F纵坐标为定值.
解:(1)①∵x=0时,y=x2+bx+c=c
∴C(0,c),OC=﹣c(c<0)
∴OA=OC=﹣c,OB=2OC=﹣2c
∴A(c,0),B(﹣2c,0)
∵抛物线y=x2+bx+c经过点A、B
∴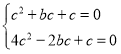 解得:
解得: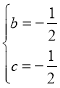
∴抛物线的解析式为y=x2﹣![]() x﹣
x﹣![]() .
.
②过点M作MD⊥AC于点D,过点D作GH∥x轴,过点A作AG⊥GH于点G,过点M作MH⊥GH于点H,如图1所示:
∴∠ADM=∠G=∠H=90°
∴Rt△ADM中,cos∠MAC=![]()
∴AM=![]() AD
AD
∴MD=![]()
∵c=![]()
∴A(![]() ,0),B(1,0),C(0,
,0),B(1,0),C(0,![]() )
)
∴OA=OC
∴∠OAC=45°
∴∠GAD=∠GAO﹣∠OAC=45°
∴△ADG为等腰直角三角形
∴∠ADG=45°
∴∠MDH=180°﹣∠ADG﹣∠ADM=45°
∴△MDH为等腰直角三角形
设AG=DG=t,则AD=![]() t
t
∴MD=4AD=![]() t
t
∴DH=MH=4t
∴xM=xA+t+4t=![]() +5t,yM=4t﹣t=3t
+5t,yM=4t﹣t=3t
∵点M在抛物线上
∴(![]() +5t)2
+5t)2![]() (
(![]() +5t)
+5t)![]() =3t
=3t
解得:t1=0(舍去),t2=![]()
∴xM=![]() +
+![]() =
=![]() ,yM=
,yM=![]()
∴点M坐标为(![]() ,
,![]() )
)
故答案为:(![]() ,
,![]() ).
).
(2)EF所在直线的纵坐标是定值,理由如下:
过点P作PQ⊥EF于点Q,如图2所示:
∵P(m,﹣2)在抛物线上
∴m2+bm+c=﹣2,即c+2=﹣m2﹣bm
∵EF∥x轴且在点P上方
∴xQ=xP=m,设yE=yF=yQ=n,n>﹣2
∴PQ=n﹣(﹣2)=n+2
∵x2+bx+c=n,整理得x2+bx+c﹣n=0
∴xE+xF=﹣b,xExF=c﹣n
∴∠PQE=∠PQF=90°
∵∠EPF=90°
∴∠EPQ+∠FPQ=∠FPQ+∠PFQ=90°
∴∠EPQ=∠PFQ
∴△EPQ∽△PFQ
∴![]()
∴PQ2=EQFQ
∴(n+2)2=(m﹣xE)(xF﹣m)
∴n2+4n+4=mxF﹣m2﹣xExF+mxE
n2+4n+4=m(xE+xF)﹣m2﹣xExF
n2+4n+4=﹣bm﹣m2﹣(c﹣n)
n2+4n+4=c+2﹣c+n
解得:n1=﹣1,n2=﹣2(舍去)
∴EF所在直线的纵坐标为﹣1,是定值.

【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
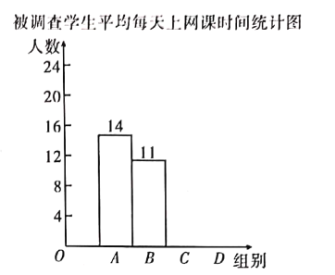
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.