题目内容
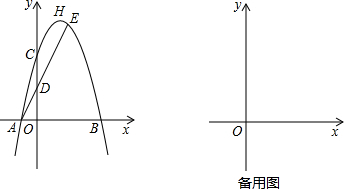
如图,已知顶点为H的抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比3:2.
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线AE交于点N,与x轴相交于点F,点P为对称轴右侧抛物线上一点,且S△PDN=4S△HDN,求点P的坐标;
(3)将抛物线向下平移n个单位后,其顶点为M,当∠AME≥90°时,求n的取值范围.
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线AE交于点N,与x轴相交于点F,点P为对称轴右侧抛物线上一点,且S△PDN=4S△HDN,求点P的坐标;
(3)将抛物线向下平移n个单位后,其顶点为M,当∠AME≥90°时,求n的取值范围.

考点:二次函数综合题
专题:压轴题
分析:(1)根据底边相等的三角形的面积的比等于高的比求出OC的长,求出点C的坐标,再根据中点定义求出点D的坐标,然后利用待定系数法求出直线AE的解析式,再求出点A的坐标,然后利用待定系数法求二次函数解析式解答;
(2)根据抛物线解析式求出顶点H的坐标,再求出点N的坐标,根据底边相等的三角形的面积的比等于对应高的比求出点P到DN的距离等于点H到DN的距离的4倍,再根据平行线分线段成比例定理求出过点P平行于AE的直线与对称轴交点到点N的距离为5,即为点F,再求出直线PF的解析式,联立抛物线解析式求解即可;
(3)过点E作EG⊥MF于G,分①点M在点G上方时,利用△MEG和△AMF相似,根据相似三角形对应边成比例列式求出MF,再根据n=FH-MF求出向下平移的最小距离;②点M在点G下方时,利用△AMF和△MEG相似,根据相似三角形对应边成比例列式求出MF,再根据n=FH+MF求出向下平移的最大距离,然后写出n的取值范围即可.
(2)根据抛物线解析式求出顶点H的坐标,再求出点N的坐标,根据底边相等的三角形的面积的比等于对应高的比求出点P到DN的距离等于点H到DN的距离的4倍,再根据平行线分线段成比例定理求出过点P平行于AE的直线与对称轴交点到点N的距离为5,即为点F,再求出直线PF的解析式,联立抛物线解析式求解即可;
(3)过点E作EG⊥MF于G,分①点M在点G上方时,利用△MEG和△AMF相似,根据相似三角形对应边成比例列式求出MF,再根据n=FH-MF求出向下平移的最小距离;②点M在点G下方时,利用△AMF和△MEG相似,根据相似三角形对应边成比例列式求出MF,再根据n=FH+MF求出向下平移的最大距离,然后写出n的取值范围即可.
解答:解:(1)∵△ABE与△ABC的面积之比3:2,点E(2,6),
∴OC=
×2=4,
∴点C的坐标为(0,4),
∵D为OC的中点,
∴点D的坐标为(0,2),
设直线AE的解析式为y=kx+b(k≠0),
则
,
解得
,
∴直线AE的解析式为y=2x+2,
令y=0,则2x+2=0,
解得x=-1,
∴点A(-1,0),
∵抛物线y=ax2+bx+c经过点A(-1,0),C(0,4),E(2,6),
∴
,
解得
,
∴抛物线的解析式y=-x2+3x+4;
(2)∵y=-x2+3x+4=-(x-
)2+
,
∴抛物线的顶点H的坐标为(
,
),
∵y=2×
+2=5,
∴点N的坐标为(
,5),
∵S△PDN=4S△HDN,
∴点P到DN的距离等于点H到DN的距离的4倍,
∵HN=
-5=
,
×4,
∴过点F平行于直线AE的直线与抛物线的交点即为点P,
设直线PF的解析式为y=2x+b,
则2×
+b=0,
解得b=-3,
∴直线PF的解析式为y=2x-3,
联立
,
解得
,
,
∵点P为对称轴右侧抛物线上一点,
∴点P的坐标为(
,
-2);
(3)如图,过点E作EG⊥MF于G,
①点M在点G上方时,由∠AME=90°易得△MEG∽△AMF,
∴
=
,
即
=
,
整理得,4MF2-24MF-5=0,
解得MF1=
,MF2=
(舍去),
∴向下平移的最小距离n=FH-MF=
-
=
,
②点M在点G下方时,由∠AME=90°易得△AMF∽△MEG,
∴
=
,
即
=
,
整理得,4MF2+24MF-5=0,
解得MF1=
,MF2=
(舍去)
∴向下平移的最大距离n=FH+MF=
+
=
,
综上所述,当∠AME≥90°时,n的取值范围是
≤m≤
.
∴OC=
| 6 |
| 3 |
∴点C的坐标为(0,4),
∵D为OC的中点,
∴点D的坐标为(0,2),
设直线AE的解析式为y=kx+b(k≠0),
则
|
解得
|
∴直线AE的解析式为y=2x+2,
令y=0,则2x+2=0,
解得x=-1,
∴点A(-1,0),
∵抛物线y=ax2+bx+c经过点A(-1,0),C(0,4),E(2,6),
∴
|
解得
|
∴抛物线的解析式y=-x2+3x+4;
(2)∵y=-x2+3x+4=-(x-
| 3 |
| 2 |
| 25 |
| 4 |
∴抛物线的顶点H的坐标为(
| 3 |
| 2 |
| 25 |
| 4 |
∵y=2×
| 3 |
| 2 |
∴点N的坐标为(
| 3 |
| 2 |
∵S△PDN=4S△HDN,
∴点P到DN的距离等于点H到DN的距离的4倍,
∵HN=
| 25 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
∴过点F平行于直线AE的直线与抛物线的交点即为点P,
设直线PF的解析式为y=2x+b,
则2×
| 3 |
| 2 |
解得b=-3,
∴直线PF的解析式为y=2x-3,

联立
|
解得
|
|
∵点P为对称轴右侧抛物线上一点,
∴点P的坐标为(
1+
| ||
| 2 |
| 29 |
(3)如图,过点E作EG⊥MF于G,
①点M在点G上方时,由∠AME=90°易得△MEG∽△AMF,
∴
| MG |
| AF |
| EG |
| MF |
即
| MF-6 | ||
1+
|
2-
| ||
| MF |
整理得,4MF2-24MF-5=0,
解得MF1=
6+
| ||
| 2 |
6-
| ||
| 2 |
∴向下平移的最小距离n=FH-MF=
| 25 |
| 4 |
6+
| ||
| 2 |
13-2
| ||
| 4 |
②点M在点G下方时,由∠AME=90°易得△AMF∽△MEG,
∴
| MG |
| AF |
| EG |
| MF |
即
| MF+6 | ||
1+
|
2-
| ||
| MF |
整理得,4MF2+24MF-5=0,
解得MF1=
-6+
| ||
| 2 |
-6-
| ||
| 2 |
∴向下平移的最大距离n=FH+MF=
| 25 |
| 4 |
-6+
| ||
| 2 |
13+2
| ||
| 4 |
综上所述,当∠AME≥90°时,n的取值范围是
13-2
| ||
| 4 |
13+2
| ||
| 4 |
点评:本题是二次函数综合题型,主要利用了三角形的面积,待定系数法求二次函数解析式,待定系数法求一次函数解析式,(2)利用三角形的面积和平行线分线段成比例定理求出过点P与AE平行的直线经过点F是解题的关键,(3)作辅助线并根据相似三角形对应边成比例求出平移的最大距离和最小距离是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE是AB的垂直平分线,则
如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE是AB的垂直平分线,则∠BDE的度数是( )
| A、15° | B、30° |
| C、45° | D、60° |
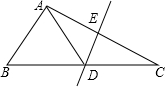 如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABC的周长为26cm.求△ABD的周长.
如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABC的周长为26cm.求△ABD的周长.