��Ŀ����
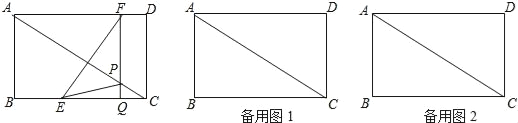
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��BC=8cm�������E�ɵ�B������BC�������C�����˶���ͬʱ��F�ɵ�D������DA�������A�����˶������ǵ��ٶȷֱ�Ϊÿ��2cm��1cm��FQ��BC���ֱ�AC��BC�ڵ�P��Q�����˶�ʱ��Ϊt�루0��t��4����
��1������EF�����˶�ʱ��t=�� ��ʱ��EF��AC��
��2������EP������EPC�����Ϊ3cm2ʱ����t��ֵ��
��3������EQP�ס�ADC����t��ֵ��
���𰸡���1��![]() �룻��2��2�룻��3��2��.
�룻��2��2�룻��3��2��.
��������
��1����ȷ����AC=10�������ó���ACB������ֵ���������Ǻ����ó�CP��CG�����ɵó�PG�����жϳ���PFG�ס�EFQ���������̼��ɵó����ۣ�
��2�����������ε�����������̼��ɵó����ۣ�
��3�����жϳ�EQ=CQ�������ó�CE=2CQ���������̼��ɵó����ۣ�
�⣺��1����ͼ1��
�ھ���ABCD�У�AB=6��BC=8�����ݹ��ɶ����ã�AC=10��
�ߡ�B=��D=��BCD=90�㣬FQ��BC��Q��
���ı���CDFQ�Ǿ��Σ�
��CQ=DF��
���˶�֪��BE=2t��DF=t��
��CQ=t��CE=BC��BE=8��2t��AF=8��t��
��EQ=CE��CQ=8��3t��
��Rt��ABC��cos��ACB=![]() ��
��
��Rt��CPQ��cos��ACB=![]() ,
,
��CP=![]() t��
t��
��EF��AC��
���CGE=90��=��ABC��
���ACB+��FEQ=90�㣬
�ߡ�ACB+��BAC=90�㣬
���FEQ=��BAC��
���ABC�ס�EQF��
��![]()
��![]() ��
��
��EQ=![]() ��
��
��8��3t=![]() ��
��
t=![]() �룻
�룻
�ʴ��ǣ�![]() �룻
�룻
��2���ɣ�1��֪��CE=8��2t��CQ=t��
��Rt��ABC��tan��ACB=![]() ��
��
��Rt��CPQ��tan��ACB=![]() ��
��
��PQ=![]() t��
t��
�ߡ�EPC�����Ϊ3cm2��
��S��EPC=![]() CE��PQ=
CE��PQ=![]() ����8��2t����
����8��2t����![]() t=3��
t=3��
��t=2�룬
����t��ֵΪ2�룻
��3���ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB��
�ߡ�EQP�ס�ADC��
���CAD=��QEP��
���ACB=��QEP��
��EQ=CQ��
��CE=2CQ��
�ɣ�1��֪��CQ=t��CE=8��2t��
��8��2t=2t��
��t=2�룮
����t��ֵΪ2�룮

 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д� Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�����Ŀ��2019 �� 3 �� 31 �գ��Ͼ������µļ۸���ʽʵʩ��ʵ�������۽��Żݣ���ͨ����ÿ�³ֿ������������������ۼƽ����� 150 Ԫʱ��ÿ�γ���������Ʊ�۴� 9��5 �ۣ��������ۼƽ� ��� 150 Ԫʱ���ﵽ�涨�������ۼƽ�����ij˴Σ�Ʊ�������ۿ����±���ʾ��
�����ۼƽ�� | �ۿ� |
| 9�� |
| 8�� |
| 9.5�� |
С���ϡ��°�ÿ�γ����ĵ�������Ʊ��Ϊ 10Ԫ��2019�� 4�·����ϡ��°�ֿ��������� 40�Σ�
��1�������
��1 �� | ��2 �� | �� | ��15�� | ��16�� | ��17�� | �� | |
�����ۼ� ��Ԫ�� | 9.5 | 19 | �� | 142.5 | 152 | �� |
span>
��2��С�����µڼ��γ˳��������ۼƽ��� 20Ԫ������һԪһ�β���ʽ������⣩
��3��С�� 4�·��ϡ��°�ֿ����������������ۼƽ��Ϊ Ԫ��