题目内容
在直角梯形ABCD中，AD⊥BC，AB⊥AD，AB=10
，AD、BC的长是方程x2-20x+75=0的两根，那么，以点D为圆心、AD为半径的圆与以点C为圆心、BC为半径的圆位置关系是______．
| 3 |
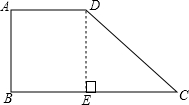
过点D作DE⊥BC于E，
∵AD、BC的长是方程x2-20x+75=0的两根，
∴解得：x1=5，x2=15，如图所示：
可得：AD=5，BC=15，
∵AD∥BC，AB⊥BC，
∴AB∥DE，
∴四边形ABED是矩形，
∴DE=AB=10
，BE=AD=5，∠DEC=90°，
∴EC=BA-BE=15-5=10，
∴CD=
=20，
∵AD+BC=20，
∴两圆的位置关系是外切．
故答案为：外切．
∵AD、BC的长是方程x2-20x+75=0的两根，
∴解得：x1=5，x2=15，如图所示：
可得：AD=5，BC=15，
∵AD∥BC，AB⊥BC，
∴AB∥DE，
∴四边形ABED是矩形，
∴DE=AB=10
| 3 |
∴EC=BA-BE=15-5=10，
∴CD=
| DE2+EC2 |
∵AD+BC=20，
∴两圆的位置关系是外切．
故答案为：外切．
练习册系列答案
名校课堂系列答案
相关题目
长线上有一点E，满足