Question

【题目】已知△ABC 是等腰直角三角形， BC AC ，ABC BAC ，直角顶点 C 在 x 轴上，一锐角顶点 B 在 y 轴上.

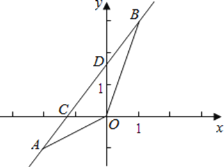
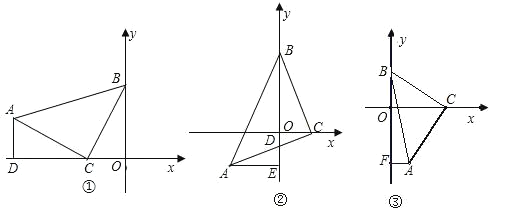
（1）如图①若 AD 于垂直 x 轴，垂足为点 D .点 C 坐标是 1, 0 ，点 A 的坐标是 3,1 ， 求点 B 的坐标.

（2）如图②，直角边 BC 在两坐标轴上滑动，若 y 轴恰好平分 ABC ， AC 与 y 轴交于点D ，过点 A 作 AE y 轴于 E ，请猜想 BD 与 AE 有怎样的数量关系，并证明你的猜想.

（3）如图③，直角边 BC 在两坐标轴上滑动，使点 A 在第四象限内，过 A 点作 AF y 轴于 F ，在滑动的过程中，两个结论①为定值；②为定值，只有一个结论成立，请你判断正确的结论加并求出定值.

Answer 1

【答案】(1) 点B的坐标是(0,2)；(2) AE=BD，理由见解析；（3）①为定值，定值为1.

【解析】

（1）只要求出Rt△ADC≌Rt△COB即可求．

（2）延长AE交BC的延长线于点F，证明△ABE≌△FBE即易求AE= AF；再证 △BCD≌△ACF，可得BD=AF，即可得结论；

（3） =1，若证明则过点A作AE⊥CO于E，证明△BOC≌△CEA即可．

(1)∵AD⊥x轴，x轴⊥y轴

∴∠ADC=∠COB=90°

∵点C坐标是(1,0),点A的坐标是(3,1)

∴AD=OC=1,OD=3

∴DC=2

在Rt△ADC和Rt△COB中

∴Rt△ADC≌Rt△COB(HL)

∴OB=CD=2

∴点B的坐标是(0,2)

(2)猜想：AE=BD，理由如下：

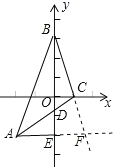
如图，延长AE、BC交于点F，

∵y轴平分∠ABC，AE⊥y轴，

∴∠ABE=∠FBE,

∴AE=EF，∴∠AEB==∠FEB=90°

∵BE=BE

∴△BEA≌△BEF

∴AF=2AE，

∵AE⊥Y轴，

∴∠EAD+∠ADE=90°，

∵∠ADE=∠BDC，

∴∠EAD+∠BDC=90°，

∵∠ACB=90°，

∴∠BDC+∠CBD=90°，

∴∠DAE=∠CBD，

在△BCD和△ACF中,

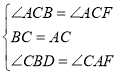
∴△BCD≌△ACF，

∴BD=AF，

∵AF=2AE，

∴BD=2AE；

∴AE=BD

(3)结论 成立理由如下：

如图3，作AE⊥OC于E，

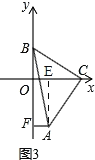
∵∠ACB=90°，

∴∠OCB+∠OCA=90°，

∵∠OBC+∠OCB=90°，

∴∠OCA=∠OBC，

在△OBC和△ECA中

.

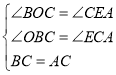∴△OBC≌△ECA，

∴OB=CE，

∵AF=OE

∴①是定值，

②，而2AF与AB的关系不知，

∴②不是定值

即：①为定值, =1.