题目内容
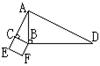
在△ABC中,点D、E分别在AB、AC上,且DE//BC,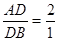 ,则S△ADE:S△ABC=_____________
,则S△ADE:S△ABC=_____________
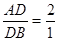 ,则S△ADE:S△ABC=_____________
,则S△ADE:S△ABC=_____________4:9
试题分析:
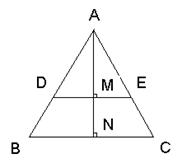
依题意知,DE∥BC,可证明△ADE∽△ABC。过点A做AN⊥BC。垂足为N。则可得AM⊥DE。垂足为点M。已知
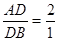 ,则AM:AN=AD:AB=2:3
,则AM:AN=AD:AB=2:3故S△ADE:S△ABC=
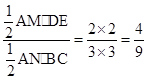
点评:本题难度较低,主要考查学生对相似三角形性质知识点的掌握。相似三角形中对应边与对应高成比例。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
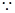 AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( )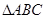 中,
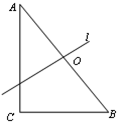
中,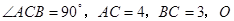 是边
是边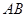 的中点,过点O的直线
的中点,过点O的直线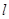 将
将