题目内容
已知正方形ABCD的边长为4,E是边CD上的一个动点,以CE为一条直角边作等腰直角三角形CEF,连接BF、FD、BD,则BD与CF的位置关系式________.
(1)如图1,当CE=4(即点E与点D重合)时,△BDF的面积为________;
(2)如图2,当CE=2(即点E为CD的中点)时,△BDF的面积为________;
(3)如图3,当CE=3时,△BDF的面积为________.

(4)如图4,根据上述计算结果,当E是CD边上任意一点时,请提出你对△BDF面积与正方形ABCD的面积之间关系的猜想;并证明你的猜想.
(5)如图5,若E是CD延长线上任意一点时,请你判断(4)中的结论是否仍然成立.
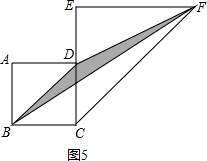
解:∵正方形ABCD和等腰直角三角形CDF,
∴BC∥AD,BC=CD=EF,
∴四边形BDFC是平行四边形,
∴BD∥CF,
故答案为:BD∥CF.
(1)解:AD=DF=4,
∴S△BDF= DF×AB=
DF×AB= ×4×4=8,
×4×4=8,
故答案为:8.
(2)解:△BDF的面积是S△BCD+S△CDF-S△BCF,…
= BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,
= ×4×4+
×4×4+ ×4×2-
×4×2- ×4×2,
×4×2,
=8,
故答案为:8.
(3)解:△BDF的面积是:S△BCD+S△CDF-S△BCF,
= BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,
= ×4×4+
×4×4+ ×4×3-
×4×3- ×4×3,
×4×3,
=8,
故答案为:8.
(4)解:S△BDF= S正方形ABCD,
S正方形ABCD,
证明:∵S正方形ABCD=AB×BC=4×4=16,
S△BDF=S△BCD+S△CDF-S△BCF,
= BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,
= ×4×4+
×4×4+ ×4×EF-
×4×EF- ×4×EF,
×4×EF,
=8,
∴S△BDF= S正方形ABCD.
S正方形ABCD.
(5)仍然成立,
理由是:∵EF=CE,
∴S正方形ABCD=AB×BC,
S△BDF=S△BCD+S△CDF-S△BCF,
= BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,
= BC×CD,
BC×CD,
∴S△BDF= S正方形ABCD.
S正方形ABCD.
分析:根据正方形的性质和等腰直角三角形的性质求出BC=EF,BC∥EF,推出平行四边形BDFC即可;
(1)根据三角形的面积公式求出即可;
(2)根据△BDF的面积=S△BCD+S△CDF-S△BCF,代入求出即可;
(3)根据△BDF的面积=S△BCD+S△CDF-S△BCF,代入求出即可;
(4)根据△BDF的面积=S△BCD+S△CDF-S△BCF和EF=CE,代入求出即可;
(5)根据△BDF的面积=S△BCD+S△CDF-S△BCF、EF=CE和正方形的面积,代入求出即可.
点评:本题综合考查了等腰直角三角形,正方形的性质,三角形的面积,平行四边形的性质和判定等知识点的应用,题型较好,用的数学思想是类比思想,考查了学生分析问题、解决问题的能力.
∴BC∥AD,BC=CD=EF,
∴四边形BDFC是平行四边形,
∴BD∥CF,
故答案为:BD∥CF.
(1)解:AD=DF=4,
∴S△BDF=
 DF×AB=
DF×AB= ×4×4=8,
×4×4=8,故答案为:8.
(2)解:△BDF的面积是S△BCD+S△CDF-S△BCF,…
=
 BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,=
 ×4×4+
×4×4+ ×4×2-
×4×2- ×4×2,
×4×2,=8,
故答案为:8.
(3)解:△BDF的面积是:S△BCD+S△CDF-S△BCF,
=
 BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,=
 ×4×4+
×4×4+ ×4×3-
×4×3- ×4×3,
×4×3,=8,
故答案为:8.
(4)解:S△BDF=
 S正方形ABCD,
S正方形ABCD,证明:∵S正方形ABCD=AB×BC=4×4=16,
S△BDF=S△BCD+S△CDF-S△BCF,
=
 BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,=
 ×4×4+
×4×4+ ×4×EF-
×4×EF- ×4×EF,
×4×EF,=8,
∴S△BDF=
 S正方形ABCD.
S正方形ABCD.(5)仍然成立,
理由是:∵EF=CE,
∴S正方形ABCD=AB×BC,
S△BDF=S△BCD+S△CDF-S△BCF,
=
 BC×CD+
BC×CD+ CD×EF-
CD×EF- BC×CE,
BC×CE,=
 BC×CD,
BC×CD,∴S△BDF=
 S正方形ABCD.
S正方形ABCD.分析:根据正方形的性质和等腰直角三角形的性质求出BC=EF,BC∥EF,推出平行四边形BDFC即可;
(1)根据三角形的面积公式求出即可;
(2)根据△BDF的面积=S△BCD+S△CDF-S△BCF,代入求出即可;
(3)根据△BDF的面积=S△BCD+S△CDF-S△BCF,代入求出即可;
(4)根据△BDF的面积=S△BCD+S△CDF-S△BCF和EF=CE,代入求出即可;
(5)根据△BDF的面积=S△BCD+S△CDF-S△BCF、EF=CE和正方形的面积,代入求出即可.
点评:本题综合考查了等腰直角三角形,正方形的性质,三角形的面积,平行四边形的性质和判定等知识点的应用,题型较好,用的数学思想是类比思想,考查了学生分析问题、解决问题的能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为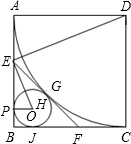 合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H
合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H (2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
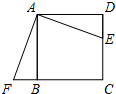
(2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. (2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒.
(2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒. 如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是