��Ŀ����
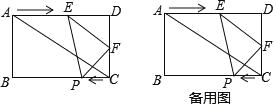
����Ŀ����ͼ1��������ȫ�ȵĺ�45���ǵ�ֱ�����ǰ�ABC��DEF������һ��ʹ���ǰ�DEF����Ƕ���D�����ǰ�ABC��б���е�O�غϣ������ǰ�ABC�̶������������ǰ�DEF�Ƶ�D��ת�����߷ֱ����߶�AB��BC�ཻ�ڵ�P��Q����˵����APD�ס�CDQ.�����������ݣ��ش��������⣺
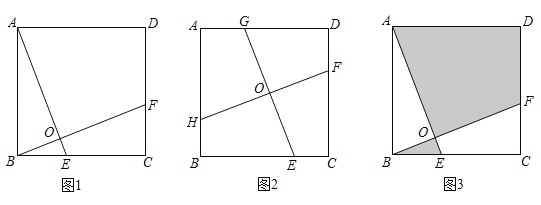
(1)��ͼ2������30���ǵ����ǰ�DEF(������EDF��30��)����Ƕ���D�������ABC(������ABC��120��)�ĵױ��е�O�غϣ�����DF��DE�ֱ����AB��BC�ཻ�ڵ�P��Q.д��ͼ�е�����������__ _ (ֱ�����ں�����)��
(2)�����������䣬�����ǰ�DEF��ת������DF��DE�ֱ����AB���ӳ��ߡ���BC�ཻ�ڵ�P��Q.�������ۻ�������������ͼ3�ϲ�ȫͼ�Σ���˵�����ɣ�
(3)��(2)�������£�����PQ����APD����DPQ�Ƿ����ƣ���˵�����ɣ�
(4)����(1)(2)�Ľ����̣����ܷ������ǰ��Ϊ��һ��������Σ�ʹ��(1)�еĽ�����Ȼ���������ܣ���˵������������Ӧ����������������ܣ����Ҫ˵�����ɣ�
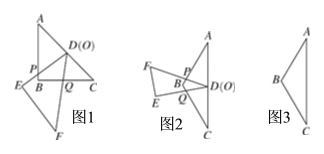
���𰸡�(1)��APD�ס�CDQ�� (2)������ͼ�����������ɼ�������(3)��APD�ס�DPQ�����ɼ�������(4)��DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ��������ɼ�����.
��������
��1��ͨ���ǵ�ת���ó���APD=��CDQ�������ɵó���APD�ס�CQD��
��2������֪�ɵ���BAC����BCA���ٸ�����֪���Ƶ��ó���APD����CDQ���̶��ɵó���APD�ס�CQD��
��3����APD�ס�DPQ���������£�����APD�ס�CDQ���ɵ�![]() ���ٸ��ݵ�DΪAC���е㣬�̶��ɵó�
���ٸ��ݵ�DΪAC���е㣬�̶��ɵó�![]() ���ٸ�����PAD����PDQ��30�㣬����֤����APD�ס�DPQ��
���ٸ�����PAD����PDQ��30�㣬����֤����APD�ס�DPQ��
��4����DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ���.
(1)�ߡ�ABC=120�㣬
���A=��C=30�㣬
�ߡ�ADP+��APD=150�㣬��ADP+��QDC=150�㣬
���APD=��CDQ��
���APD�ס�CDQ��
�ʴ�Ϊ����APD�ס�CDQ��
(2)��������ͼ���������£�
��AB��BC��
���BAC����BCA��
�ߡ�ABC��120�㣬
���BAC����BCA��30�㣬
���ADP����APD��180�㣭30�㣽150�㣬
�ߡ�EDF��30�㣬
���ADP����CDQ��150�㣬
���APD����CDQ��
���APD�ס�CDQ��
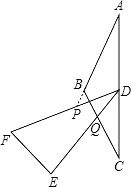
(3)��APD�ס�DPQ���������£�
��ͼ���ߡ�APD�ס�CDQ��
��![]() ��
��
����DΪAC���е㣬
��CD��AD��
��![]() ����
����![]() ��
��
���ߡ�PAD����PDQ��30�㣬
���APD�ס�DPQ��
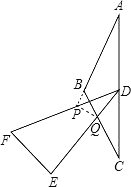
(4)��DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ�����
���ɣ��ߡ�ABC��180�㣭2����
���A����C������
�ߡ�ADP����APD��180�㣭������ADP����QDC��180�㣭����
���APD����CDQ��
���ߡ�A����C��
���APD�ס�CDQ.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ijУ�ٰ�İ��꼶ѧ����ѧ������������![]() ����Ŀ:���ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ÿ����Ŀ�÷ֶ���һ���ٷֱ����������ܷ֣��ָܷߵĻ�ʤ���±�ΪС��С����λͬѧ�ĵ÷��������λ:�֣�:
����Ŀ:���ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ÿ����Ŀ�÷ֶ���һ���ٷֱ����������ܷ֣��ָܷߵĻ�ʤ���±�ΪС��С����λͬѧ�ĵ÷��������λ:�֣�:
���ɰ�ƴͼ | Ȥ���ɽ� | ��ѧӦ�� | |
�� |
|
|
|
�� |
|
|
|
![]() �����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ������÷ֱַ�
�����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ������÷ֱַ�![]() ����������ܷ֣�����˭�ܻ�ʤ?
����������ܷ֣�����˭�ܻ�ʤ?
![]() �����ɰ�ƴͼ��
�����ɰ�ƴͼ��![]() ���㣬С�� ������ܡ������ܡ�����ʤ��
���㣬С�� ������ܡ������ܡ�����ʤ��