题目内容
【题目】数学课堂上老师对一道课外作业进行了延拓，请同学们解答下列问题：
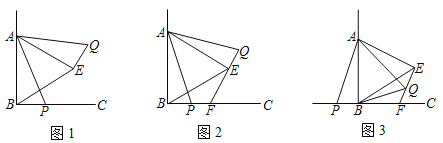
（1）如图1：∠ABC＝90°，△ABE是等边三角形，AB＝6
，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE，则BP与QE的数量关系是：BP QE．
（2）如图2：在（1）的条件下，延长QE交射线BC于点F，若设BP＝x，点Q到射线BC的距离为y，试写出y关于x的函数关系式．
（3）如图3：在（1）的条件中，如果改点P为直线BC上的任意一个动点，其他条件均不变，请探究AP在旋转过程中，△ABQ周长是否存在最小值，如果有，请求出这个值；如果不存在，请说明理由．
【答案】（1）＝；（2）y＝
x+3
（x＞0）；（3）存在，△ABQ周长最小值为18+6．
【解析】
（1）由“SAS”可证△ABP≌△AEQ，可得BP=QE；
（2）在图2中，过点F作FG⊥BE于点G．过点Q作QH⊥BC，垂足为H，由（1）可知△ABP≌△AEQ，可得∠AEQ=∠ABP=90°，由直角三角形的性质可求EF=6，可得QF=QE+EF=x+6，由直角三角形的性质可求解；
（3）先确定点Q的位置，点Q在过点E且垂直于AE的直线上运动，由三边关系可得当点Q在BN上时，△ABQ周长有最小值，即可求解．
（1）∵将线段AP绕点A逆时针旋转60°得到线段AQ，
∴AP＝AQ，∠PAQ＝60°，
∵△ABE是等边三角形，
∴AB＝AE，∠BAE＝∠PAQ＝60°，
∴∠BAP＝∠EAQ，且AP＝AQ，AB＝AE，
∴△ABP≌△AEQ（SAS）
∴BP＝QE，
故答案为：＝；
（2）在图2中，过点F作FG⊥BE于点G．过点Q作QH⊥BC，垂足为H．
∵△ABE是等边三角形，
∴BE＝AB＝6．
由（1）可知△ABP≌△AEQ，
∴∠AEQ＝∠ABP＝90°，且∠AEB＝60°，
∴∠BEF＝30°，
∴∠EBF＝∠BEF＝30°，
∴BF＝EF，
∵FG⊥BE，
∴BG＝
＝3，
∵∠EBF＝30°，
∴BF＝2GF，BG＝GF，
∴GF＝3，BF＝6，
∴EF＝6，
∵QE＝BP＝x，
则QF＝QE+EF＝x+6，
在Rt△QHF中，∠QFH＝60°，
∴∠FQH＝30°，
∴FH＝
QF，
∴y＝QH＝FH＝（x+6）．（x＞0）
即y关于x的函数关系式是：y＝x+3（x＞0）
（3）由（1）可知：△ABP≌△AEQ，
∴∠AEQ＝∠ABP＝90°，
∴点Q在过点E且垂直于AE的直线上运动，
如图3，延长AE交BC于点N，连接AF，QN，
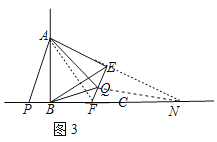
∵∠ABC＝90°，∠BAN＝60°，
∴∠ANB＝30°，
∴AN＝2AB＝12，且AE＝AB＝6，
∴EN＝AN﹣AE＝6，
∴AE＝EN，且EF⊥AN，
∴AQ＝QN，
∵△ABQ周长＝AB+AQ+BQ＝6+BQ+QN≥6+BN，
∴当点Q在BN上时，△ABQ周长有最小值，
∵BN＝AB＝18，
∴△ABQ周长最小值＝18+6．
