题目内容
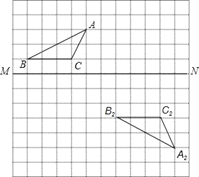
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
【答案】(1)见解析;(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;(3)作图见解析,点P的坐标为(1,0).
【解析】
(1)依据轴对称的性质,即可得到△ABC关于MN对称的图形△A1B1C1;
(2)依据△A2B2C2与△A1B1C1的位置,即可得到平移的方向和距离;
(3)连接AB2,交x轴于P,连接A1P,依据两点之间,线段最短,即可得到PA1+PB2最小,进而得到点P的坐标.
解:(1)如图所示,△A1B1C1即为所求;
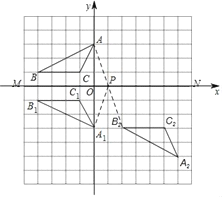
(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;
(3)如图,连接AB2,交x轴于P,连接A1P,则PA1+PB2最小,
此时,点P的坐标为(1,0).

练习册系列答案
相关题目