题目内容
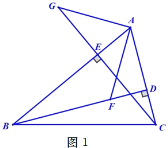
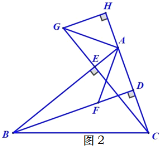
【题目】如图，某校区内有甲、乙两块大小一样的长方形地块，地块长30m，宽25m，现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分)，余下的部分绿化．现已知ABCD1m，EFGH1m，记甲、乙地块的绿化面积分别为S1、S2，则S1、S2的大小关系是（ ）
A.S1<S2B.S1=S2C.S1>S2D.无法确定
【答案】C
【解析】
根据图片，我们可以看到绿化面积就是长方形的面积减去阴影部分的面积，分别求出两个长方形中阴影部分的面积，就可以得出答案．
解：由题意可知：两个图中左右方向的平行四边形小路的面积都是：30×1=30（m），
两个图中上下方向的平行四边形小路的面积都是：25×1=25（m），
图甲中的重叠部分是1×1=1（m），
，
如图，分别做PR∥CD、NS∥CD交QD于R、S，过点N做NO⊥PR于O，
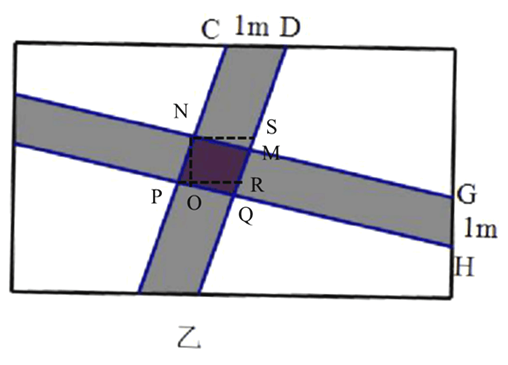
则
，四边形RSNS是平行西边形，
PR=NS=CD=1m，NO＜GH，GH=1m，
在平行四边形PQMN中，PQ∥MN，
，
易证
，
，
，
，
，
；
故答案为：C．
练习册系列答案
相关题目
