题目内容
如图,直角坐标系中,已知点A(3,0),B(t,0)(0<t<| 3 | 2 |
(1)求证:△OBC≌△FBA;?
(2)一抛物线经过O、F、A三点,试用t表示该抛物线的解析式;?
(3)设题(2)中抛物线的对称轴l与直线AF相交于点G,若G为△AOC的外心,试求出抛物线的解析式;?
(4)在题(3)的条件下,问在抛物线上是否存在点P,使该点关于直线AF的对称点在x轴上
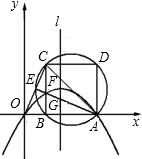 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由.
分析:(1)这两个三角形中,已知的条件有∠BCE=∠BAE(圆周角定理),一组直角,BC=AB,因此构成了全等三角形的判定条件,因此两三角形全等.
(2)本题的关键是求出F的坐标,根据(1)的全等三角形可得出OB=BF=t,由此可得出F的坐标,然后代入抛物线中即可用待定系数法求出抛物线的解析式.
(3)易知:正方形的边长为3-t,因此C(t,3-t),可设G的坐标为(1.5,b),根据GO=GC可用t表示出G的纵坐标,然后代入抛物线的直线AF的即解析式中即可求出t的值.即能确定出抛物线的解析式.
(4)根据(3)得出的条件,易证得CF:BF=AC:AB=
,根据三角形内角平分线判定定理,可得出AF是∠CAB的角平分线,如果存在P点,那么P必为抛物线与直线AC的交点,可联立两个函数的解析式求出交点坐标即可.
(2)本题的关键是求出F的坐标,根据(1)的全等三角形可得出OB=BF=t,由此可得出F的坐标,然后代入抛物线中即可用待定系数法求出抛物线的解析式.
(3)易知:正方形的边长为3-t,因此C(t,3-t),可设G的坐标为(1.5,b),根据GO=GC可用t表示出G的纵坐标,然后代入抛物线的直线AF的即解析式中即可求出t的值.即能确定出抛物线的解析式.
(4)根据(3)得出的条件,易证得CF:BF=AC:AB=
| 2 |
解答:解:(1)证明:∵∠BCE=∠BAE,∠FAB=∠OBC=90°,AB=BC
∴△OBC≌△FBA.
(2)由(1)易知:OF=OB=t,
因此F(t,t),
设抛物线的解析式为y=ax(x-3),
则有:t=at(t-3),a=
,
∴抛物线的解析式为y=
x2-
x.
(3)易知:C(t,3-t)
设G点坐标为(
,h),由于GC=OG,
则有(
-t)2+(h-3+t)2=(
)2+h2
解得h=
.
设直线AF的解析式为y=kx+b,
则有:
,
解得
,
∴直线AF的解析式为y=
x-
.
由于直线AF过G点,
则有当x=
时,
=
×
-
,
解得t=
,
由于0<t<
,
∴t=
∴抛物线的解析式为y=-
x2+
x.
(4)由(3)知,BF=t=
=
(3
-3),CF=3-2t=3
-3.
∴
=
=
∴AF是∠CBA的角平分线,
∴若存在P点,则P点必为直线AC与抛物线的交点.
易知:直线AC的解析式为:y=-x+3.
则有
,
解得
,
,
∴存在P点,其坐标为(
,
).
∴△OBC≌△FBA.
(2)由(1)易知:OF=OB=t,
因此F(t,t),
设抛物线的解析式为y=ax(x-3),
则有:t=at(t-3),a=
| 1 |
| t-3 |
∴抛物线的解析式为y=
| 1 |
| t-3 |
| 3 |
| t-3 |
(3)易知:C(t,3-t)
设G点坐标为(
| 3 |
| 2 |
则有(
| 3 |
| 2 |
| 3 |
| 2 |
解得h=
| 3-2t |
| 2 |
设直线AF的解析式为y=kx+b,
则有:
|
解得
|
∴直线AF的解析式为y=
| t |
| t-3 |
| 3t |
| t-3 |
由于直线AF过G点,
则有当x=
| 3 |
| 2 |
| 3-2t |
| 2 |
| t |
| t-3 |
| 3 |
| 2 |
| 3t |
| t-3 |
解得t=
6±3
| ||
| 2 |
由于0<t<
| 3 |
| 2 |
∴t=
6-3
| ||
| 2 |
∴抛物线的解析式为y=-
| ||
| 3 |
| 2 |
(4)由(3)知,BF=t=
6-3
| ||
| 2 |
| 2 |
| 2 |
| 2 |
∴
| CF |
| BF |
| AC |
| AB |
| 2 |
∴AF是∠CBA的角平分线,
∴若存在P点,则P点必为直线AC与抛物线的交点.
易知:直线AC的解析式为:y=-x+3.
则有
|
解得
|
|
∴存在P点,其坐标为(
3
| ||
| 2 |
6-3
| ||
| 2 |
点评:本题主要考查了正方形的性质、圆、全等三角形的判定、轴对称图形等知识点.综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
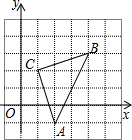 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: