题目内容
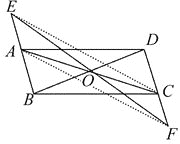
【题目】如图,平行四边形ABCD中,点O是AC与BD的交点,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:△AOE≌△COF.
(2)请连接EC,AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.
【答案】（1）证明见解析；（2）当满足EF=AC时,四边形AECF是矩形，理由见解析
【解析】(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.又∠AOE=∠COF,
∴△AOE≌△COF.
(2)连接EC,AF,则EF与AC满足EF=AC时,四边形AECF是矩形.
理由如下:
由(1)可知△AOE≌△COF,
∴OE=OF.
∵AO=CO,
∴四边形AECF是平行四边形
∵EF=AC,
∴四边形AECF是矩形.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
