题目内容
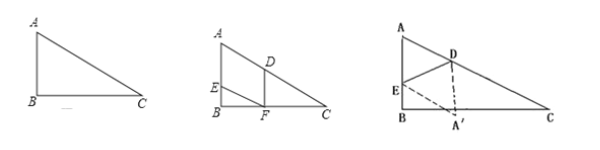
【题目】(本小题12分)如图1,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图2,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?
(4)如图3,连接DE,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
【答案】(1)AE=t , AD=12-2t ;(2)四边形AEFD是平行四边形,理由见解析; (3)t=3秒或t=![]() 秒;(4)t=4.
秒;(4)t=4.
【解析】
试题分析:(1)根据点E以每秒1cm的速度运动,同时点D以每秒2cm的速度运动,运动时间为t秒,可
得AE=t ,CD=2t,所以可得AD=12-2t ;(2)当DF⊥BC,且DF= AE 时,四边形AEFD是平行四边
形;(3)根据题意可知∠DFE<90°,所以分当∠EDF=90°时和当∠DEF=90°时两种情况讨论,利用直角三
角形中30°角的性质解答即可;(4)由(2)可知四边形AEFD可以是平行四边形,所以满足AE=AD可得四
边形AEA′D为菱形,然后解方程即可.
试题解析:解:(1)AE=t , AD=12-2t (2分)
(2)∵DF⊥BC,∠C=30°
∴ DF=![]() CD=
CD=![]() ×2t = t
×2t = t
∵ AE =t
∴ DF= AE
∵ ∠ABC=90°, DF⊥BC
∴ DF∥AE
∴ 四边形AEFD是平行四边形; (3分)
(3)①显然∠DFE<90°;
②如图①′,
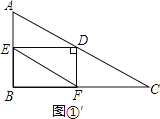
当∠EDF=90°时,四边形EBFD为矩形,
此时 AE=![]() AD,
AD,
∴t=![]() (122t),
(122t),
∴t=3;
③如图①″,
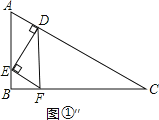
当∠DEF=90°时,此时∠ADE=90°
∴∠AED=90°-∠A=30°
∴AD=![]() AE,
AE,
∴122t=![]() t,
t,
∴t=![]() ;
;
综上:当t=3秒或t=![]() 秒时,△DEF为直角三角形; (4分)
秒时,△DEF为直角三角形; (4分)
(4)如图(3),
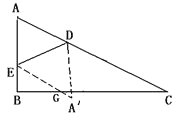
若四边形AEA′D为菱形,则AE=AD
∴t=12-2t
∴t=4
∴当t=4时,四边形AEA′D为菱形 (3分)

 名校课堂系列答案
名校课堂系列答案