题目内容

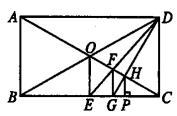
（1）阅读下列材料，补全证明过程。

如图，已知在矩形ABCD中，AC、BD相交于点O，

OE⊥BC于点E，连结DE交OC于点F，作FG⊥BC于点G。

求证：点G是线段BC的一个三等分点。

证明：在矩形ABCD中，OE⊥BC，DC⊥BC，∴ OE//DC。

∵ ＝，∴ ＝＝。

∴ ＝。

（2）请你仿照上面的画法，在原图上画出BC的一个四等分点。（要求：保留作图痕迹，

不写画法及证明过程）

 

答案：
解析：

（1）∵FG⊥BG，DC⊥BC。

∴FG//DC。

∴ ＝＝

∵ AB＝DC，∴ ＝

又∵FG//AB，∴ ＝＝

（2）画法如图，P点为所求作的点。

 


练习册系列答案
相关题目
请阅读下列材料，规定一种运算：
.
ab
cd
.
=ab-bc，例如：
.
23
45
.
=2×5-3×4=-2，按照这种运算的规定，当x=
 
时，
.
x
1
2
-x
21
.
=
2
3
．
阅读下列材料并解决有关问题：
我们知道，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=O，分别求得x=-1，x=2（称-1，2分别为|x+1|与|x-2|的零点值）．在实数范围内，零点值x=-1和，x=2可将全体实数分成不重复且不遗漏的如下3种情况：
（1）x＜-1；（2）-1≤x＜2；（3）x≥2．从而化简代数式|x+1|+|x-2|可分以下3种情况：
（1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1≤x＜2时，原式=x+1-（x-2）=3；
（3）当x≥2时，原式=x+1+x-2=2x-1．
综上讨论，原式=
-2x+1(x＜-1)
3(-1≤x＜2)
2x-1(x≥2)
．
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|x-4|的零点值；
（2）化简代数式|x+2|+|x-4|．
26、阅读下列材料并完成填空：
你能比较两个数20042005和20052004的大小吗？为了解决这个问题，先把问题一般化，即比较nn+1和（n+1）n的大小（n≥1，n是整数），然后从分析n=1，n=2，n=3，…，这些简单情形入手，从中发现规律，经过归纳，猜想出结论．
（1）通过计算，比较下列①-⑥各组的两个数的大小．（在横线上填“＞”、“=”、“＜”）
①12
＜
21②23
＜
32③34
＞
43
④45
＞
54⑤56
＞
65⑥67
＞
76…；
（2）从上面各小题的结果经过归纳，可以猜出nn+1和（n+1）n的大小关系；
（3）根据上面归纳猜想的一般结论，可以得到20042005
＞
20052004（在横线上填“＞”、“=”、“＜”）
阅读理解题：阅读下列材料，关于x的方程：x+
1
x
=c+
1
c
的解是x1=c，x2=
1
c
；
x-
1
x
=c-
1
c
（即x+
-1
x
=c+
-1
c
）的解是x1=c，x2=-
1
c
；x+
2
x
=c+
2
c
的解是：x1=c，x2=
2
c
，…
（1）观察上述方程及其解的特征，直接写出关于x的方程x+
m
x
=c+
m
c
（m≠0）的解，并利用“方程的解”的概念进行验证；
（2）通过（1）的验证所获得的结论，你能解出关于x的方程：x+
2
x-1
=a+
2
a-1
的解吗？若能，请求出此方程的解；若不能，请说明理由．
请阅读下列材料：
我们规定一种运算：
.
ac
bd
.
=ad-bc，例如：
.
23
45
.
=2×5-3×4=10-12=-2．按照这种运算的规定，请解答下列问题：（1）直接写出
.
-12
-20.5
.
的计算结果；
（2）当x取何值时，
.
x0.5-x
12x
.
=0；
（3）若
.
0.5x-1y
83
.
=
.
x-y
0.5-1
.
=-7，直接写出x和y的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网