题目内容
 如图,D是△ABC的边BC上一点,DE⊥AC于点E,DF⊥AB于点F,且DE=DF.
如图,D是△ABC的边BC上一点,DE⊥AC于点E,DF⊥AB于点F,且DE=DF.(1)下列结论中正确的有
②③④
②③④
(填上所有正确结论代号)①AD是△ABC的中线
②AD是△ABC的角平分线
③S△ABD:S△ACD=AB:AC=BD:DC
④AE=AF.
(2)在图中连接EF,求证:AD垂直平分EF.
分析:(1)由DE⊥AC于点E,DF⊥AB于点F,且DE=DF,根据角平分线的判定,即可证得AD是△ABC的角平分线;由三角形的面积公式,根据等高三角形的面积比等于对应底的比,即可证得S△ABD:S△ACD=AB:AC=BD:DC;易证得∠ADF=∠ADE,然后由角平分线的性质,可证得AE=AF;
(2)根据(1)可证得AD是△ABC的角平分线且AE=AF,然后由三线合一,可证得AD垂直平分EF.
(2)根据(1)可证得AD是△ABC的角平分线且AE=AF,然后由三线合一,可证得AD垂直平分EF.
解答:解:(1)∵DE⊥AC,DF⊥AB,DE=DF,
∴AD是△ABC的角平分线,
故②正确;
∵S△ABD:S△ACD=(
AB•DF):(
AC•DE)=AB:AC=BD:DC,
故③正确;
∵∠DAF=∠DAE,∠AFD=∠AED=90°,
又∵∠ADF=90°-∠DAF,∠ADE=90°-∠DAE,
∴∠ADF=∠ADE,
∴AE=AF;
故④正确;
∵BD不一定等于CD,
∴①错误;
故答案为:②③④;
 (2)∵DE⊥AC,DF⊥AB,DE=DF,
(2)∵DE⊥AC,DF⊥AB,DE=DF,
∴AD是∠ABC的平分线,
又∵∠ADF=90°-∠DAF,∠ADE=90°-∠DAE,
∴∠ADF=∠ADE,
∴AE=AF,
∴AD垂直平分EF.
∴AD是△ABC的角平分线,
故②正确;
∵S△ABD:S△ACD=(
| 1 |
| 2 |
| 1 |
| 2 |
故③正确;
∵∠DAF=∠DAE,∠AFD=∠AED=90°,
又∵∠ADF=90°-∠DAF,∠ADE=90°-∠DAE,
∴∠ADF=∠ADE,
∴AE=AF;
故④正确;
∵BD不一定等于CD,
∴①错误;
故答案为:②③④;
 (2)∵DE⊥AC,DF⊥AB,DE=DF,
(2)∵DE⊥AC,DF⊥AB,DE=DF,∴AD是∠ABC的平分线,
又∵∠ADF=90°-∠DAF,∠ADE=90°-∠DAE,
∴∠ADF=∠ADE,
∴AE=AF,
∴AD垂直平分EF.
点评:此题考查了角平分线的性质与判定以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
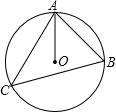 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
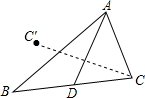 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=