题目内容
如图,在直角坐标系中,Rt△AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),把△AOB绕O点按逆时针方向旋转90°得到△COD。
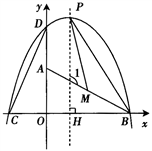
(1)求C,D两点的坐标;
(2)求经过C,D,B三点的抛物线的解析式;
(3)设(2)中抛物线的顶点为P,AB的中点为M(2,1),试判断△PMB是钝角三角形,直角三角形还是锐角三角形,并说明理由.
(2)求经过C,D,B三点的抛物线的解析式;
(3)设(2)中抛物线的顶点为P,AB的中点为M(2,1),试判断△PMB是钝角三角形,直角三角形还是锐角三角形,并说明理由.
解:(1)由旋转的性质可知:OC=OA=2,OD=OB=4,
∴C、D两点的坐标分别是C(-2,0),D(0,4);
(2)设所求抛物线的解析式为y=ax2+bx+c,
根据题意,得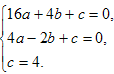
解得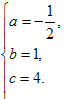
∴所求抛物线的解析式为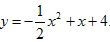 ;
;
(3)如图,△PMB是钝角三角形,图中,PH是抛物线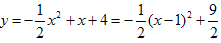 的对称轴,
的对称轴,
M、P点的坐标分别为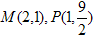
∴点M在PH的右侧,
∵∠PHB=90°,∠1>90°,∠PMB>∠1,
∴∠PMB>90°,
则△PMB为钝角三角形。
∴C、D两点的坐标分别是C(-2,0),D(0,4);
(2)设所求抛物线的解析式为y=ax2+bx+c,
根据题意,得
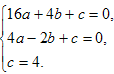
解得
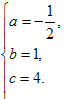
∴所求抛物线的解析式为
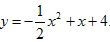 ;
;(3)如图,△PMB是钝角三角形,图中,PH是抛物线
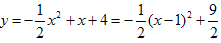 的对称轴,
的对称轴,M、P点的坐标分别为
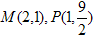
∴点M在PH的右侧,
∵∠PHB=90°,∠1>90°,∠PMB>∠1,
∴∠PMB>90°,
则△PMB为钝角三角形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: