题目内容
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

【答案】![]()
【解析】
试题分析:延长FB到点M,使BM=DG,连接CM
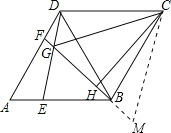
∵△ABD是等边三角形,
∴AD=BD,∠A=∠ABD=60°,
在△AED与△DFB中,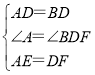 ,
,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∵∠CDG=∠ADC-∠ADE=120°-∠ADE,∠CBM=120°-∠DBF,
∴∠CBM=∠CDG,
∵△DBC是等边三角形,
∴CD=CB,
在△CDG和△CBM中,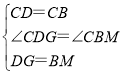 ,
,
∴△CDG≌△CBM,
∴∠DCG=∠BCM,CG=CM,
∴∠GCM=∠DCB=60°,
∴△CGM是等边三角形,
∴CG=GM=BG+BM=BG+DG,
∵(a+b)2=a2+b2+2ab=9,
∴a+b=3,
∴CG=3,
∴GH=![]() CG=
CG=![]() .
.

练习册系列答案
相关题目



