题目内容
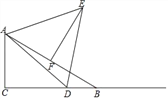
【题目】如图,在△ABC中,∠C=90°,点D、点E为BC边上两点,且AC=DC,
(1)若∠EAC=∠EAF,EF⊥AB且AB=5,BC=4,求线段DE的长度;
(2)若EF⊥AD于点P,CF⊥AE于点Q,且AE=CF,求证:![]() DE+PF=AP
DE+PF=AP

【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由勾股定理可求AC=3,由“AAS”可证△ACE≌△AFE,可得AC=AF=3,EC=EF,由勾股定理可求CE的长,即可求DE的长;
(2)如图,连接DF,由“SAS”可证△ACE≌△CDF,可得CE=DF,∠ACE=∠CDF=90°,设AC=CD=2a,由等腰直角三角形的性质可得AD=2![]() a,EC=DF=DE=a,EF=
a,EC=DF=DE=a,EF=![]() a,DP=EP=PF=
a,DP=EP=PF=![]() a,即可得结论.
a,即可得结论.
解:∵AB=5,BC=4,∠C=90°,
∴AC=![]() =3,
=3,
∵AE=AE,∠EAC=∠EAF,∠C=∠EFA=90°,
∴△ACE≌△AFE(AAS)
∴AC=AF=3,EC=EF,
∴CD=AC=3,BF=2,
∵BE2=BF2+EF2,
∴BE2=4+(4﹣BE)2,
∴BE=![]() ,
,
∴EC=![]() ,
,
∴DE=CD﹣CE=![]() ;
;
(2)如图,连接DF,
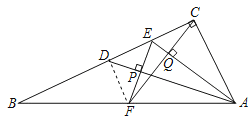
∵CF⊥AE,
∴∠ACB=∠CQA=90°
∴∠ACQ+∠ECQ=90°,∠ACQ+∠CAQ=90°,
∴∠ECQ=∠CAQ,且CD=AC,CF=AE,
∴△ACE≌△CDF(SAS)
∴CE=DF,∠ACE=∠CDF=90°,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠CDA=45°,
∴∠FDA=∠CDA=45°,且EF⊥AD,
∴∠EDP=∠DEP=45°=∠PDF=∠DFP,
∴DP=PE=PF,DF=DE,
∴DE=DF=EC,
设AC=CD=2a,
∴AD=2![]() a,EC=DF=DE=a,
a,EC=DF=DE=a,
∴EF=![]() a,DP=EP=PF=
a,DP=EP=PF=![]() a,
a,
∴AP=AD﹣DP=![]() a,
a,
∴![]() DE+PF=
DE+PF=![]() a+
a+![]() a=
a=![]() a=AP
a=AP
∴![]() DE+PF=AP.
DE+PF=AP.

【题目】温州瓯柑,声名远播.某经销商欲将仓库的120吨瓯柑运往A,B两地销售.运往A,B两地的瓯柑(吨)和每吨的运费如下表.设仓库运往A地的瓯柑为x吨,且x为整数.
瓯柑(吨) | 运费(元/吨) | |
A地 | x | 20 |
B地 | 30 |
(1)设仓库运往A,B两地的总运费为y元.
①将表格补充完整.
②求y关于x的函数表达式.
(2)若仓库运往A地的费用不超过运往A,B两地费用的![]() ,求总运费的最小值.
,求总运费的最小值.