题目内容
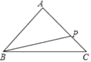
【题目】在△ABC中，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是（ ）
A. 5 B. 6 C. 4 D. 4.8
【答案】D
【解析】
根据点到直线的连线中，垂线段最短，得到当BP垂直于AC时，BP的长最小，过A作等腰三角形底边上的高AD，利用三线合一得到D为BC的中点，在直角三角形ADC中，利用勾股定理求出AD的长，进而利用面积法即可求出此时BP的长．
根据垂线段最短，得到BP⊥AC时，BP最短，
过A作AD⊥BC，交BC于点D，
∵AB＝AC，AD⊥BC，
∴D为BC的中点，又BC＝6，
∴BD＝CD＝3，
在Rt△ADC中，AC＝5，CD＝3，
根据勾股定理得：AD＝
＝4，
又∵S△ABC＝
BCAD＝BPAC，
∴BP＝
＝4.8．
故选：D．
练习册系列答案
相关题目
