题目内容
【题目】在图1、图2的网格中,每个小四边形均为正方形,且边长是1.如果三角形的顶点均在网格交点处,我们称这样的三角形为格点三角形.下面的三角形均为格点三角形.
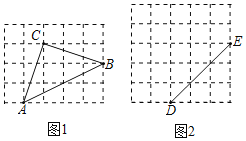
(1)如图1,试判断△ABC的形状,并说明理由;
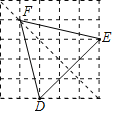
(2)在图2的网格中,请你以DE为底边,画一个面积为7.5的等腰三角形.
【答案】(1) △ABC是等腰直角三角形,理由见解析;(2)见解析.
【解析】
(1)根据勾股定理逆定理求解可得;
(2)先作出线段DE的中垂线,再在此直线上找到满足条件的格点,从而得出答案.
解:(1)△ABC是等腰直角三角形.
∵AC2=BC2=12+32=10,AB2=22+42=20,
∴AC2+BC2=AB2,
∴△ABC是等腰直角三角形;
(2)如图所示,△DEF即为所求.
设所求三角形的高为h,
∵DE=![]() ,
,
∴![]() ,
,
∴h=![]() ,
,
∴腰长为=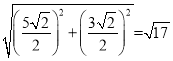 ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目