题目内容
【题目】下图的方格纸中有若干个点,若A、B两点关于过某点的直线对称,这个点可能是( ).

A.P1B.P2C.P3D.P4
【答案】C
【解析】
根据两点的对称轴即两点连线的垂直平分线,利用勾股定理分别求出选项中各点到A、B的距离,再根据垂直平分线的性质即可判断.
解:连接P1B,P2A,P3A,P3B,P4B,设正方形的边长为1,P4O=a,如下图所示
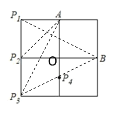
∵A、B两点关于过某点的直线对称
∴此点在AB的垂直平分线上
∴此点到A、B的距离相等
由图可知:P1A=1
根据勾股定理:P1B=![]()
∴P1A≠P1B,故A选项不符合题意;
由图可知:P2B=2
根据勾股定理:P2A=![]()
∴P2B≠P2A,故B选项不符合题意;
根据勾股定理:P3A=![]()
P3B=![]()
∴P3A= P3B,故C选项符合题意;
由图可知P4A=1+a
根据勾股定理:P4B=![]()
当P4A=P4B时,即1+a=![]()
解得:a=0(与图不符)
∴P4A≠P4B,故D选项不符合题意.
故选C.

练习册系列答案
相关题目