Question

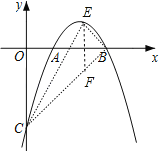
【题目】如图，二次函数y＝ax2+bx﹣3的图象与x轴的两个交点分别为A（1，0）、B（3，0），与y轴的交点为C．

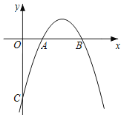
（1）求这个二次函数的表达式；

（2）在x轴上方的二次函数图象上，是否存在一点E使得以B、C、E为顶点的三角形的面积为？若存在，求出点E坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x2+4x﹣3；（2）存在，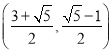

【解析】

（1）设交点式y＝a（x﹣1）（x﹣3），化为一般式得到3a＝﹣3，解得a＝﹣1，从而得到抛物线解析式；

（2）先确定C（0，﹣3），作EF∥y轴交直线BC于F，如图，利用直线平移得到直线BC的解析式为y＝x﹣3，设E（x，﹣x2+4x﹣3），则F（x，x﹣3），利用三角形面积公式得到S△BCE＝EF3＝﹣x2+x＝，然后解方程求出x即可得到满足条件的E点坐标．

解：（1）抛物线的解析式为y＝a（x﹣1）（x﹣3），即y＝ax2﹣4ax+3a，

∵3a＝﹣3，解得a＝﹣1，

∴抛物线解析式为y＝﹣x2+4x﹣3；

（2）存在．

当x＝0时，y＝﹣x2+4x﹣3＝-3，

∴C（0，﹣3），

作EF∥y轴交直线BC于F，如图，

∵B（3，0），C（0，﹣3）；

得直线BC的解析式为y＝x﹣3，

设E（x，﹣x2+4x﹣3），则F（x，x﹣3），

∴EF＝﹣x2+4x﹣3﹣（x﹣3）＝﹣x2+3x，

∴S△BCE＝EF3＝﹣x2+x，

即﹣x2+x＝，解得x1＝，x2＝

当x＝时，y＝﹣x2+4x﹣3＝，此时E点坐标为（，），

当x＝时，y＝﹣x2+4x﹣3＝，此时E点坐标为（，），

∵E在x轴上方，此情况不符合题意；

综上所述，E点坐标为（，）．