Question

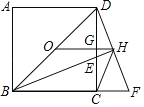
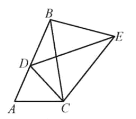
【题目】如图，四边形ABCD是正方形，点E是边AB上一点，延长AD至F使DF＝BE，连接CF．

（1）求证：∠BCE＝∠DCF；

（2）过点E作EG∥CF，过点F作FG∥CE，问四边形CEGF是什么特殊的四边形，并证明．

Answer 1

【答案】(1)见解析；(2) 四边形CEGF是正方形，证明见解析.

【解析】

（1）由正方形的性质得到∠B＝∠CDF＝90°，BC＝CD，根据全等三角形的判定和性质即可得到结论；

（2）根据已知条件得到四边形CEGF是平行四边形，根据全等三角形的性质得到CE＝CF，证得四边形CEGF是菱形，求得∠ECF＝∠BCD＝90°，于是得到结论．

（1）证明：∵四边形ABCD是正方形，

∴∠B＝∠ADC＝∠BCD＝90°，BC＝CD，

∴∠B＝∠CDF＝90°，

在△BCE和△DCF中，，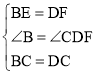

∴△BCE≌△DCF（SAS），

∴∠BCE＝∠DCF；

（2）四边形CEGF是正方形，

证明：∵EG∥CF，FG∥CE，

∴四边形CEGF是平行四边形，

∵△BCE≌△DCF，

∴CE＝CF，

∴四边形CEGF是菱形，

∵∠BCE＝∠DCF，

∴∠ECF＝∠BCD＝90°，

∴四边形CEGF是正方形．