题目内容
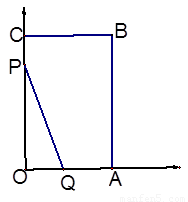
 如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=
如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=| k | x |
(1)若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求k的值.
(2)若OA=2,OC=4,当四边形AOFE的面积最大时,求点E、F的坐标.
分析:(1)点E、F反比例函数y=
(k>0)图象上的点,S△OAE=S△OCF=
,再由S1+S2=2即可求出k的值;
(2)四边形OABC为矩形,OA=2,OC=4,可设E(
,2),F(4,
),再由S四边形AOFE=S矩形OABC-S△BEF-S△OCF即可得出关于k的一元二次方程,由二次函数的顶点坐标可得出当k=4时,四边形AOFE的面积最大,故可得出E、F两点的坐标.
| k |
| x |
| k |
| 2 |
(2)四边形OABC为矩形,OA=2,OC=4,可设E(
| k |
| 2 |
| k |
| 4 |
解答:解:(1)∵点E、F反比例函数y=
(k>0)图象上的点,
∴S△OAE=S△OCF=
,
∴S1+S2=
+
=2,解得,k=2;
(2)∵四边形OABC为矩形,OA=2,OC=4,
∴设E(
,2),F(4,
),
∴BE=4-
,BF=2-
,
∴S△BEF=
(4-
)(2-
)=
k2-k+4,
∵S△OAE=S△OCF=
×4×
=
,S矩形OABC=2×4=8,
∴S四边形AOFE=S矩形OABC-S△BEF-S△OCF=8-(
k2-k+4)-
=-
k2+
k+4,
=-
(k-4)2+5
∵a<0,
∴开口向下,S四边形AOFE有最大值
∴当k=4时,四边形AOFE的面积最大,
∴AE=
=2,CF=
=1.
∴E(2,2),F(4,1).
| k |
| x |
∴S△OAE=S△OCF=
| k |
| 2 |
∴S1+S2=
| k |
| 2 |
| k |
| 2 |
(2)∵四边形OABC为矩形,OA=2,OC=4,
∴设E(
| k |
| 2 |
| k |
| 4 |
∴BE=4-
| k |
| 2 |
| k |
| 4 |
∴S△BEF=
| 1 |
| 2 |
| k |
| 2 |
| k |
| 4 |
| 1 |
| 16 |
∵S△OAE=S△OCF=
| 1 |
| 2 |
| k |
| 4 |
| k |
| 2 |
∴S四边形AOFE=S矩形OABC-S△BEF-S△OCF=8-(
| 1 |
| 16 |
| k |
| 2 |
| 1 |
| 16 |
| 1 |
| 2 |
=-
| 1 |
| 16 |
∵a<0,
∴开口向下,S四边形AOFE有最大值
∴当k=4时,四边形AOFE的面积最大,
∴AE=
| k |
| 2 |
| k |
| 4 |
∴E(2,2),F(4,1).
点评:本题考查的是反比例函数综合题,根据题意用k表示出E、F两点的坐标,再根据三角形的面积公式求解是解答此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
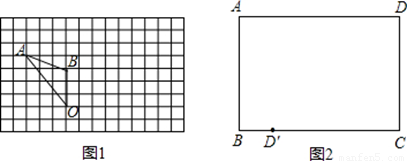
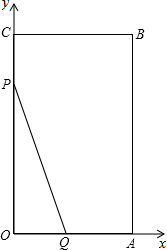 已知:在平面直角坐标系中矩形OABC如图,且A(6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动t秒,且速度均为每秒2个单位长度,设S△OPQ=S.
已知:在平面直角坐标系中矩形OABC如图,且A(6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动t秒,且速度均为每秒2个单位长度,设S△OPQ=S.
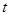 秒,且速度均为每秒2个单位长度,设
秒,且速度均为每秒2个单位长度,设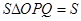 .
.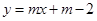 平分矩形OABC面积,求
平分矩形OABC面积,求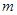 的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)