题目内容
(2008•西城区一模)已知抛物线C1:y=ax2-2amx+am2+2m+1(a>0,m>1)的顶点为A,抛物线C2的对称轴是y轴,顶点为点B,且抛物线C1和C2关于P(1,3)成中心对称.(1)用m的代数式表示抛物线C1的顶点坐标;
(2)求m的值和抛物线C2的解析式(含有字母a);
(3)设抛物线C2与x轴正半轴的交点是C,当△ABC为等腰三角形时,求a的值.

【答案】分析:(1)观察抛物线解析式,可发现前三项提取公因式a后,可配成完全平方式,由此可将抛物线的解析式化为顶点坐标式,即可得到C1的顶点坐标.
(2)由于B点在y轴上,且A、B关于P点呈中心对称,那么点P为线段AB的中点,即A横坐标为P点的2倍,可据此求出m的值,进而可表示出A、B的坐标,由于抛物线C1和C2关于P(1,3)成中心对称,那么它们的开口方向相反,顶点关于P对称,根据顶点B的坐标即可表示出抛物线C2的解析式.
(3)首先设出点C的横坐标,然后表示出AB、AC、BC的长,分①AB=AC、②AB=BC、③AC=BC三种情况讨论即可.
解答: 解:(1)由于抛物线C1:y=ax2-2amx+am2+2m+1=a(x-m)2+2m+1,
解:(1)由于抛物线C1:y=ax2-2amx+am2+2m+1=a(x-m)2+2m+1,
故抛物线C1的顶点A(m,2m+1).
(2)分别过A、P作y轴的垂线,设垂足为F、E;
∵A、B关于P点呈中心对称,
∴AB=2BP;
∴PE是△ABF的中位线,即AF=2PE=2,
故m=2,A(2,5);
设直线AP的解析式为y=kx+b,则有:
 ,
,
解得 ,
,
∴直线AP:y=2x+1,
故B(0,1);
由于抛物线C1和C2关于P(1,3)成中心对称,且顶点B(0,1),则:
抛物线C2:y=-ax2+1.
(3)设C(x,0),已知A(2,5),B(0,1);
AB2=(2-0)2+(5-1)2=20,
AC2=(2-x)2+52=x2-4x+29,
BC2=(0-x)2+1=x2+1;
若△ABC为等腰三角形,则有:
①AB=AC,由于AB=2 ,而A(2,5),因此AC≥5,故AB<AC,此种情况不成立;
,而A(2,5),因此AC≥5,故AB<AC,此种情况不成立;
②AB=BC,则AB2=BC2,有:
x2+1=20,解得x=± (负值舍去);
(负值舍去);
将x= 代入抛物线C2的解析式中,得:-19a+1=0,即a=
代入抛物线C2的解析式中,得:-19a+1=0,即a= ;
;
③AC=BC,则AC2=BC2,有:
x2-4x+29=x2+1,解得x=7;
将x=7代入抛物线C2的解析式中,得:-49a+1=0,即a= ;
;
故△ABC为等腰三角形时,a的值为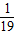 或
或 .
.
点评:此题主要考查了抛物线顶点坐标的求法、函数图象的几何变换、等腰三角形的判定等知识,同时考查了分类讨论的数学思想,难度较大.
(2)由于B点在y轴上,且A、B关于P点呈中心对称,那么点P为线段AB的中点,即A横坐标为P点的2倍,可据此求出m的值,进而可表示出A、B的坐标,由于抛物线C1和C2关于P(1,3)成中心对称,那么它们的开口方向相反,顶点关于P对称,根据顶点B的坐标即可表示出抛物线C2的解析式.
(3)首先设出点C的横坐标,然后表示出AB、AC、BC的长,分①AB=AC、②AB=BC、③AC=BC三种情况讨论即可.
解答:
 解:(1)由于抛物线C1:y=ax2-2amx+am2+2m+1=a(x-m)2+2m+1,
解:(1)由于抛物线C1:y=ax2-2amx+am2+2m+1=a(x-m)2+2m+1,故抛物线C1的顶点A(m,2m+1).
(2)分别过A、P作y轴的垂线,设垂足为F、E;
∵A、B关于P点呈中心对称,
∴AB=2BP;
∴PE是△ABF的中位线,即AF=2PE=2,
故m=2,A(2,5);
设直线AP的解析式为y=kx+b,则有:
 ,
,解得
 ,
,∴直线AP:y=2x+1,
故B(0,1);
由于抛物线C1和C2关于P(1,3)成中心对称,且顶点B(0,1),则:
抛物线C2:y=-ax2+1.
(3)设C(x,0),已知A(2,5),B(0,1);
AB2=(2-0)2+(5-1)2=20,
AC2=(2-x)2+52=x2-4x+29,
BC2=(0-x)2+1=x2+1;
若△ABC为等腰三角形,则有:
①AB=AC,由于AB=2
 ,而A(2,5),因此AC≥5,故AB<AC,此种情况不成立;
,而A(2,5),因此AC≥5,故AB<AC,此种情况不成立;②AB=BC,则AB2=BC2,有:
x2+1=20,解得x=±
 (负值舍去);
(负值舍去);将x=
 代入抛物线C2的解析式中,得:-19a+1=0,即a=
代入抛物线C2的解析式中,得:-19a+1=0,即a= ;
;③AC=BC,则AC2=BC2,有:
x2-4x+29=x2+1,解得x=7;
将x=7代入抛物线C2的解析式中,得:-49a+1=0,即a=
 ;
;故△ABC为等腰三角形时,a的值为
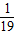 或
或 .
.点评:此题主要考查了抛物线顶点坐标的求法、函数图象的几何变换、等腰三角形的判定等知识,同时考查了分类讨论的数学思想,难度较大.

练习册系列答案
相关题目
 (2013•西城区一模)近年来,北京郊区依托丰富的自然和人文资源,大力开发建设以农业观光园为主体的多类型休闲旅游项目,京郊旅游业迅速崛起,农民的收入逐步提高.以下是根据北京市统计局2013年1月发布的“北京市主要经济社会发展指标”的相关数据绘制的统计图表的一部分.
(2013•西城区一模)近年来,北京郊区依托丰富的自然和人文资源,大力开发建设以农业观光园为主体的多类型休闲旅游项目,京郊旅游业迅速崛起,农民的收入逐步提高.以下是根据北京市统计局2013年1月发布的“北京市主要经济社会发展指标”的相关数据绘制的统计图表的一部分.