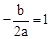题目内容
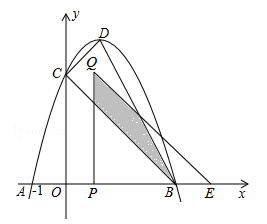
如图,抛物线 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式及点C的坐标;
(2)点E为线段OC上一动点,以OE为边在第一象限内作正方形OEFG,当正方形的顶点F恰好落在线段AC上时,求线段OE的长;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动.设平移的距离为t,正方形DEFG的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(4)在上述平移过程中,当正方形DEFG与△ABC的重叠部分为五边形时,请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围;并求出当t为何值时,S有最大值,最大值是多少?

 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.(1)求该抛物线的函数关系表达式及点C的坐标;
(2)点E为线段OC上一动点,以OE为边在第一象限内作正方形OEFG,当正方形的顶点F恰好落在线段AC上时,求线段OE的长;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动.设平移的距离为t,正方形DEFG的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(4)在上述平移过程中,当正方形DEFG与△ABC的重叠部分为五边形时,请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围;并求出当t为何值时,S有最大值,最大值是多少?

(1) 。C(6,0)。
。C(6,0)。
(2)OE=2。
(3)存在满足条件的t.理由见解析
(4)当t=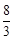 时,S取得最大值,最大值为1。
时,S取得最大值,最大值为1。
 。C(6,0)。
。C(6,0)。(2)OE=2。
(3)存在满足条件的t.理由见解析
(4)当t=
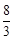 时,S取得最大值,最大值为1。
时,S取得最大值,最大值为1。试题分析:(1)利用待定系数法求出抛物线的解析式,令y=0解方程,求出点C的坐标。
(2)如答图1,由△CEF∽△COA,根据比例式列方程求出OE的长度。
(3)如答图2,若△DMN是等腰三角形,可能有三种情形,需要分类讨论。
(4)当正方形DEFG与△ABC的重叠部分为五边形时,如答图3,由S=S正方形DEFG﹣S梯形MEDN﹣S△FJK求出S关于t的表达式,然后由二次函数的性质求出其最值。
解:(1)∵抛物线
 经过点A(0,3),B(2,3),
经过点A(0,3),B(2,3),∴
 ,解得:
,解得: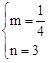 。
。∴抛物线的解析式为:
 。
。令y=0,即
 ,解得x=6或x=﹣4。
,解得x=6或x=﹣4。∵点C位于x轴正半轴上,∴C(6,0)。
(2)当正方形的顶点F恰好落在线段AC上时,如答图所示:

设OE=x,则EF=x,CE=OC﹣OE=6﹣x.
∵EF∥OA,∴△CEF∽△COA。
∴
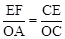 ,即
,即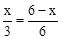 。
。解得x=2.∴OE=2。
(3)存在满足条件的t.理由如下:
如答图,

易证△CEM∽△COA,
∴
 ,即
,即 ,得
,得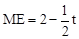 。
。过点M作MH⊥DN于点H,
则DH=ME=
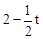 ,MH=DE=2。
,MH=DE=2。易证△MNH∽△COA,∴
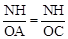 ,即
,即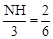 ,得NH=1。
,得NH=1。∴DN=DH+HN=
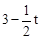 。
。在Rt△MNH中,MH=2,NH=1,由勾股定理得:MN=
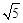 。
。当△DMN是等腰三角形时:
①若DN=MN,则
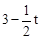 =
=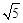 ,解得t=
,解得t=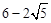 。
。②若DM=MN,则DM2=MN2,即22+(
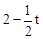 )2=(
)2=(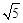 )2,解得t=2或t=6(不合题意,舍去)。
)2,解得t=2或t=6(不合题意,舍去)。③若DM=DN,则DM2=DN2,即22+(
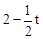 )2=(
)2=(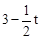 )2,解得t=1。
)2,解得t=1。综上所述,当t=1、2或
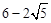 时,△DMN是等腰三角形。
时,△DMN是等腰三角形。(4)当正方形DEFG与△ABC的重叠部分为五边形时,如答图,

设EF、DG分别与AC交于点M、N,
由(3)可知:ME=
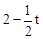 ,DN=
,DN=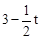 .
.设直线BC的解析式为y=kx+b,
将点B(2,3)、C(6,0)代入得:
 ,解得
,解得 。
。∴直线BC的解析式为
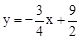 。
。设直线BC与EF交于点K,
∵xK=t+2,∴
 。
。∴
 。
。设直线BC与GF交于点J,
∵yJ=2,∴2=
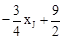 ,得
,得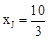 。
。∴FJ=xF﹣xJ=t+2﹣
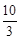 =t﹣
=t﹣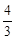 。
。∴S=S正方形DEFG﹣S梯形MEDN﹣S△FJK=DE2﹣
 (ME+DN)•DE﹣
(ME+DN)•DE﹣ FK•FJ
FK•FJ=22﹣
 [(2﹣
[(2﹣ t)+(3﹣
t)+(3﹣ t)]×2﹣
t)]×2﹣ (
(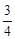 t﹣1)(t﹣
t﹣1)(t﹣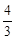 )
) .
.过点G作GH⊥y轴于点H,交AC于点I,则HI=2,HJ=
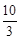 ,
,∴t的取值范围是:2<t<
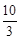 。
。∴S与t的函数关系式为:S
 (2<t<
(2<t<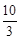 )。
)。S
 ,
,∵
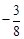 <0,且2<
<0,且2<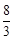 <
<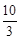 ,∴当t=
,∴当t=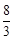 时,S取得最大值,最大值为1。
时,S取得最大值,最大值为1。
练习册系列答案
相关题目
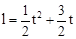 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.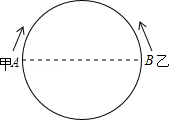
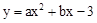 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.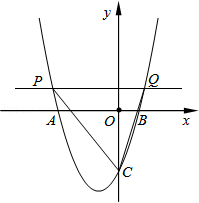
 的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点(2,2)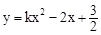 (
(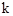 是常数)
是常数)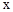 轴只有一个交点,求
轴只有一个交点,求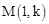 在某反比例函数的图像上,要使该反比例函数和二次函数
在某反比例函数的图像上,要使该反比例函数和二次函数 随
随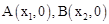 两点,且
两点,且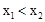 ,
,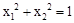 ,在
,在