题目内容
 已知:如图,四边形ABCD内接于⊙O,若∠BOD=120°,OB=1,则∠BAD=________度,∠BCD=________度,弧BCD的长=________.
已知:如图,四边形ABCD内接于⊙O,若∠BOD=120°,OB=1,则∠BAD=________度,∠BCD=________度,弧BCD的长=________.
60 120 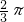
分析:已知了圆心角∠BOD的度数,利用圆周角与圆心角的关系,可求出∠BAD的度数;根据圆内接四边形的性质可求出∠BCD的度数;根据弧长计算公式可求得弧BCD的长.
解答:∵∠BOD=120°,
∴∠BAD= ∠BOD=
∠BOD= ×120°=60°;
×120°=60°;
∵四边形ABCD内接于⊙O,
∴∠BCD=180°-∠BAD=180°-60°=120°;
∵∠BOD=120°,OB=1,
∴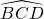 的长=
的长= =
= π.
π.
点评:本题考查弧长计算公式、圆内接四边形的性质、圆心角、圆周角的应用能力.
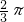
分析:已知了圆心角∠BOD的度数,利用圆周角与圆心角的关系,可求出∠BAD的度数;根据圆内接四边形的性质可求出∠BCD的度数;根据弧长计算公式可求得弧BCD的长.
解答:∵∠BOD=120°,
∴∠BAD=
 ∠BOD=
∠BOD= ×120°=60°;
×120°=60°;∵四边形ABCD内接于⊙O,
∴∠BCD=180°-∠BAD=180°-60°=120°;
∵∠BOD=120°,OB=1,
∴
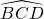 的长=
的长= =
= π.
π.点评:本题考查弧长计算公式、圆内接四边形的性质、圆心角、圆周角的应用能力.

练习册系列答案
相关题目
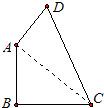 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.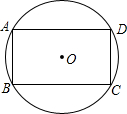 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF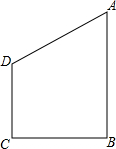 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.