题目内容
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

【答案】(1)补图见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据要求画出图象即可;
(2)根据点B、D关于AP对称得AP垂直平分BD,故ED=EB,从而得证;
(3)连接AD,由线段垂直平分线的性质得AD=AB,ED=EB,可证∠1=∠ABE;由AB=AC得AD=AC,所以∠1=∠ACE,从而得证.
(1)如图;
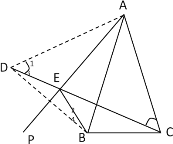
(2)∵ 点B、D关于AP对称
∴ AP垂直平分BD
∴ ED=EB
∴ CD=CE+ED=CE+EB;
(3)连接AD
∵ AP垂直平分BD
∴ AD=AB=AC
∴ ∠1=∠ACE ∠1+∠EDB=∠ABE +∠EBD
∵ ED=EB
∴ ∠EDB =∠EBD
∴ ∠1=∠ABE
∴ ∠ABE=∠ACE .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?