题目内容
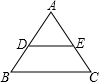
如图，已知等边△ABC，点O是BC上任意一点，OE、OF分别与两边垂直，等边三角形的高为1，则OE+OF的值为
- A.0.5
- B.1
- C.2
- D.不确定
B
分析：利用等边三角形的特殊角求出OE与OF的和，可得出其与三角形的高相等，进而可得出结论．
解答：∵OE⊥AB，OF⊥AC，∠B=∠C=60°，
∴OE=OB•sin60°=
OB，同理OF=OC．
∴OE+OF=（OB+OC）=BC．
在等边△ABC中，高h=AB．
∴OE+OF=h．
故选B．
点评：熟练掌握等边三角形的性质．
分析：利用等边三角形的特殊角求出OE与OF的和，可得出其与三角形的高相等，进而可得出结论．
解答：∵OE⊥AB，OF⊥AC，∠B=∠C=60°，
∴OE=OB•sin60°=
OB，同理OF=OC．∴OE+OF=
（OB+OC）=BC．在等边△ABC中，高h=
AB．∴OE+OF=h．
故选B．
点评：熟练掌握等边三角形的性质．
练习册系列答案
相关题目
（2013•黄浦区二模）如图，已知等边△ABC的边长为1，设
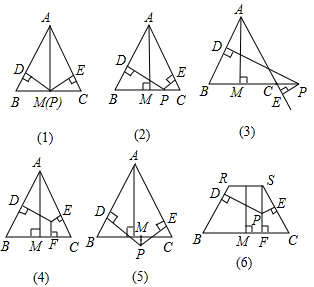
如图，已知等边三角形ABC的边长为10，点P、Q分别为边AB、AC上的一个动点，点P从点B出发以1cm/s的速度向点A运动，点Q从点C出发以2cm/s的速度向点A运动，连接PQ，以Q为旋转中心，将线段PQ按逆时针方向旋转60°得线段QD，若点P、Q同时出发，则当运动