题目内容
【题目】如图,已知点A(4,0),B(0,![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
【答案】
(1)
解:设直线AB的解析式为y=kx+b,
∵A(4,0),B(0,![]() ),
),
∴![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:![]() ;
;
(2)
解:
∵在Rt△DEF中,∠EFD=30°,ED=2,
∴EF=![]() ,DF=4,
,DF=4,
∵点D与点A重合,
∴D(4,0),
∴F(2,![]() ),
),
∴G(3,![]() ),
),
∵反比例函数![]() 经过点G,
经过点G,
∴k=![]() ,
,
∴反比例函数的解析式为:![]() ;
;
(3)
解:
经过点G的反比例函数的图象能同时经过点F;理由如下:
∵点F在直线AB上,
∴设F(t,![]() ),
),
又∵ED=2,
∴D(t+2,![]() ),
),
∵点G为边FD的中点.
∴G(t+1,![]() ),
),
若过点G的反比例函数的图象也经过点F,
设解析式为![]() ,
,
则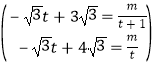 ,
,
整理得:(![]() )(t+1)=(
)(t+1)=(![]() )t,
)t,
解得:t=![]() ,
,
∴m=![]() ,
,
∴经过点G的反比例函数的图象能同时经过点F,这个反比例函数解析式为:![]() .
.
【解析】(1)设直线AB的解析式为y=kx+b,把点A、B的坐标代入,组成方程组,解方程组求出k、b的值即可;
(2)由Rt△DEF中,求出EF、DF,在求出点D坐标,得出点F、G坐标,把点G坐标代入反比例函数求出k即可;
(3)设F(t,﹣![]() t+4
t+4![]() ),得出D、G坐标,设过点G和F的反比例函数解析式为y=
),得出D、G坐标,设过点G和F的反比例函数解析式为y=![]() ,用待定系数法求出t、m,即可得出反比例函数解析式.
,用待定系数法求出t、m,即可得出反比例函数解析式.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目







