题目内容
【题目】如图1,在平面直角坐标系中,△OAB是等边三角形,O为坐标原点,点A的坐标是(3,0),点C在OA上且OC=1,连接BC.一动点P从点A出发,沿折线A→B→O的方向向终点O运动,记点P移动的路程为m.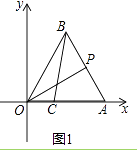
(1)当点P在线段AB上运动时,连接OP,求满足△BPO≌△OCB的m值;
(2)连接PC,求△OPC的面积s关于m的函数表达式;
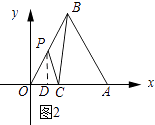
(3)如图2,过点P作边AB的垂线l,并以直线l为对称轴,作线段AC的对称线段A1C1 . 请写出在点P的运动过程中,线段A1C1与y轴有交点时m的取值范围.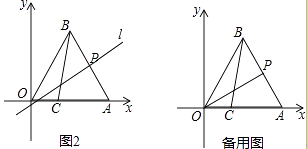
【答案】
(1)
解:∵△BPO≌△OCB,
∴BP=OC=1.
∴m=AB﹣BP=3﹣1=2
(2)
解:①如图1所示:当点P在AB上运动时,过点P作PD⊥OA.
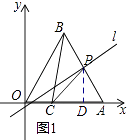
∵∠OAP=60°,∠PDA=90°,
∴∠APD=30°.
∴PD= ![]() PA
PA ![]() m.
m.
∴S= ![]() ×1×
×1× ![]() m=
m= ![]() m;
m;
②如图2所示:当点P在OB上时,过点P作PD⊥OA.
∵OP=AB+OB﹣m=6﹣m,
∴PD= ![]() (6﹣m),
(6﹣m),
∴S= ![]() ×1×
×1× ![]() (6﹣m)=
(6﹣m)= ![]() (6﹣m).
(6﹣m).
综上所述,S与m的函数关系式为S= 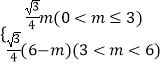
(3)
解:如图3所示:当点C的对应点C′落在y轴上时.
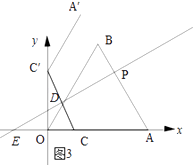
由翻折的性质可知:CC′⊥PE,DC=DC′,
又∵PE⊥AB,
∴DC∥PA.
∴∠C′CO=∠A=60°.
∴∠CC′O=30°.
∴CC′=2OC=2.
∴DC=1.
∵在△DCE中,∠EDC=90°,∠DCE=60°,
∴∠DEC=30°.
∴EC=2DC=2.
∴EC=CA.
∵DC∥AB,
∴ ![]() =
= ![]() .
.
∴AP=2.即m=2.
如图4所示:当点A的对称点A′在y轴上时.
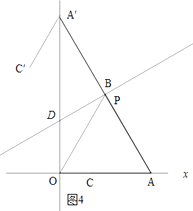
∵点A与点A′关于直线PD对称,
∴PA=PA′.
∵∠A=60°,∠AOA′=90°,
∴∠AA′O=30°.
∴AA′=2OA=6.
∴PA=3.
∴点B与点P重合,此时m=3.
如图5所示:当点P在OB上,点C′在y轴上.
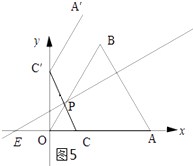
∵∠PCO=60°,∠POC=60°,
∴△OPC为等边三角形.
∴PO=OC=1.
∴PB=2.
∴m=PB+AB=5.
∴线段A1C1与y轴有交点时m的取值范围是2≤m≤5
【解析】(1)由全等三角形的性质可知BP=OC,由m=AB﹣PB求解即可;(2)过点P作PD⊥OA,垂足为D,三角形OPC的面积S= ![]() OCDP,然后分为点P在AB和OB上两种情况求得PD的长,从而得到S与m的函数关系式;(3)求得点A′或点C′恰好在y轴上时m的值,从而可确定出m的范围.
OCDP,然后分为点P在AB和OB上两种情况求得PD的长,从而得到S与m的函数关系式;(3)求得点A′或点C′恰好在y轴上时m的值,从而可确定出m的范围.
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案