题目内容
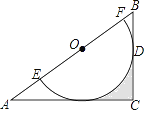
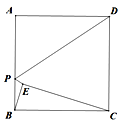
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
【答案】![]()
【解析】
根据正方形的性质得到∠ABC=90°,推出∠BEC=90°,得到点E在以BC为直径的半圆上移动,如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形AFGB,则点D的对应点是F,连接FO交AB于P,交⊙O于E,则线段EF的长即为PD+PE的长度最小值,根据勾股定理即可得到结论.
解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,
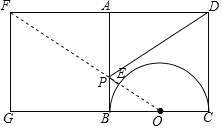
作正方形ABCD关于直线AB对称的正方形AFGB,
则点D的对应点是F,
连接FO交AB于P,交半圆O于E,
则线段EF的长即为PD+PE的长度最小值,
∵∠G=90°,FG=BG=AB=6,
∴OG=9,
∴OF=![]() =
=![]() ,
,
∴EF=![]() ,
,
故PD+PE的长度最小值为![]() ,
,
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
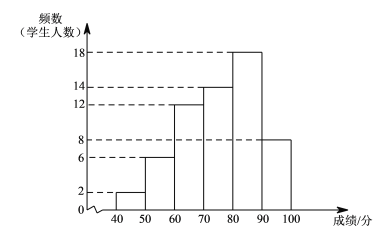
![]() .A课程成绩在
.A课程成绩在![]() 这一组是:
这一组是:
70 71 71 71 76 76 77 78 ![]()
![]() 79 79 79
79 79 79 ![]()
![]() .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过![]() 分的人数.
分的人数.