题目内容
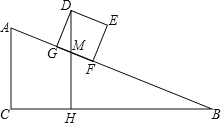
【题目】已知四边形![]() 为
为![]() 的内接四边形,直径
的内接四边形,直径![]() 与对角线
与对角线![]() 相交于点
相交于点![]() ,作
,作![]() 于
于![]() ,
,![]() 与过
与过![]() 点的直线相交于点
点的直线相交于点![]() ,
,![]() .
.
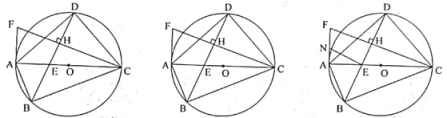
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)根据直径所对的圆周角为90°,得到∠ADC=90°,根据直角三角形两锐角互余得到∠DAC+∠DCA=90°,再根据同弧或等弧所对的圆周角相等,可得到∠FAD+∠DAC=90°,即可得出结论;
(2)连接OD.根据圆周角定理和角平分线定义可得∠DOA=∠DOC,即可得出结论;
(3)连接OD交CF于M,作EP⊥AD于P.可求出AD=4,AF∥OM.根据三角形中位线定理得出OM=![]() AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
(1)∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°.
∵![]() ,
,
∴∠ABD=∠DCA.
∵∠FAD=∠ABD,
∴∠FAD=∠DCA,
∴∠FAD+∠DAC=90°,
∴CA⊥AF,
∴AF为⊙O的切线.

(2)连接OD.
∵![]() ,
,
∴∠ABD=![]() ∠AOD.
∠AOD.
∵![]() ,
,
∴∠DBC=![]() ∠DOC.
∠DOC.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠DOA=∠DOC,
∴DA=DC.
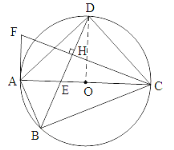
(3)连接OD交CF于M,作EP⊥AD于P.
∵AC为⊙O的直径,
∴∠ADC=90°.
∵DA=DC,
∴DO⊥AC,
∴∠FAC=∠DOC=90°,AD=DC=![]() =4,
=4,
∴∠DAC=∠DCA=45°,AF∥OM.
∵AO=OC,
∴OM=![]() AF.
AF.
∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°,
∴∠ODE=∠OCM.
∵∠DOE=∠COM,OD=OC,
∴△ODE≌△OCM,
∴OE=OM.
设OM=m,
∴OE=m,![]() ,
,![]() ,
,
∴![]() .
.
∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,
∴∠AEN=∠ADE.
∵∠EAN=∠DPE,
∴△EAN∽△DPE,
∴![]() ,
,
∴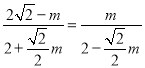 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:![]() .
.

 阅读快车系列答案
阅读快车系列答案