Question

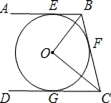
【题目】如图，AB为⊙O的直径，点C，D为上的点，且＝，延长AD，BC相交于点E，连接OD交AC于点F．

（1）求证：△ABC≌△AEC；

（2）若OA＝3，BC＝4，求AD的长．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）先根据等弧所对的圆周角相等得∠CAE＝∠CAB，再根据ASA证明即可．
（2）连接BD交OC于K，作OH⊥BC于H．求出OK的长，利用三角形的中位线定理即可解决问题．

（1）证明：∵＝，

∴∠CAE＝∠CAB，

∵AB是直径，

∠ACB＝∠ACE＝90°，

∵AC＝AC，

∴△ABC≌△AEC（ASA）．

（2）连接BD交OC于K，作OH⊥BC于H．

∵OH⊥BC，

∴CH＝HB＝2，

∵OB＝3，

∴OH＝＝，

∵＝，

∴OC⊥BD，DK＝KB，

∵BCOH＝OCBK，

∴BK＝，

∴OK＝＝，

∵OA＝OB，DK＝KB，

∴AD＝2OK＝．