题目内容
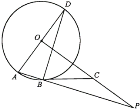
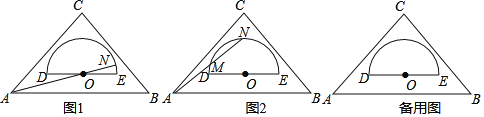
【题目】如图1是一块内置量角器的等腰直角三角板,它是一个轴对称图形.已知量角器所在的半圆O的直径DE与AB之间的距离为1,DE=4,AB=8,点N为半圆O上的一个动点,连结AN交半圆或直径DE于点M.
(1)当AN经过圆心O时,求AN的长;
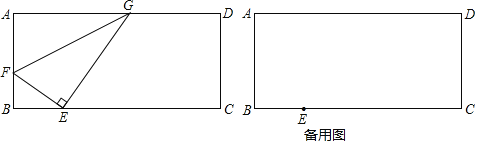
(2)如图2,若N为量角器上表示刻度为90°的点,求△MON的周长;
(3)当![]() 时,求△MON的面积.
时,求△MON的面积.
【答案】(1)AN=![]() +2;(2)
+2;(2)![]() ;(3)
;(3)![]() 或1﹣
或1﹣![]() .
.
【解析】
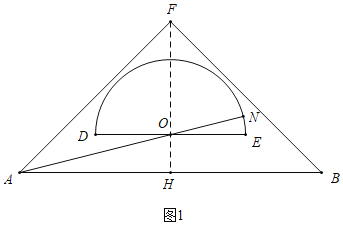
(1)如图1中,连接FO延长FO交AB于H.则FH⊥AB,FH⊥DE.解直角三角形求出AO即可解决问题.
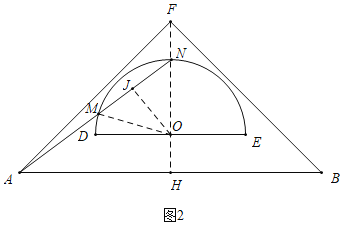
(2)如图2中,连接OM,作OJ⊥MN.利用相似三角形的性质求出NJ,再利用垂径定理求出MN即可解决问题.
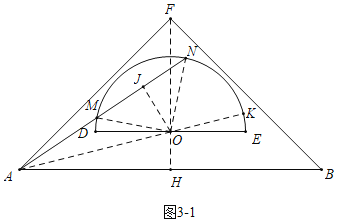
(3)分两种情形:如图3﹣1中,连接AO,延长AO交⊙O于K,作OJ⊥MN于J,连接OM,ON.设AM=MN=x,OJ=y,构建方程组即可解决问题.如图3﹣2中,连接ON,作NJ⊥AB于J交DE于K.想办法求出OM,NK即可解决问题.
(1)如图1中,连接FO延长FO交AB于H.则FH⊥AB,FH⊥DE.
∵DE=4,
∴⊙O的半径为2,
∵FA=FB,FH⊥AB,
∴AH=HB=4,
在![]() 中,OH=1,AH=4,
中,OH=1,AH=4,
∴![]() ,
,
∴![]() ;
;
(2)如图2中,连接OM,作OJ⊥MN于J.
在![]() 中, AH=4,
中, AH=4,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 公共,
公共,
∴△OJN∽△AHN,
∴![]() ,即
,即![]() ,
,
∴JN=![]() ,
,
∵OJ⊥MN,OM=ON,
∴JM=JN,
∴MN=2JN=![]() ,
,
∴△MON的周长=2+2+![]() =
=![]() ;
;
(3)如图3﹣1中,连接AO并延长AO交⊙O于K,作OJ⊥MN于J,连接OM,ON.
∵![]() ,
,
∴AM=MN=![]() ,
,
设AM=MN=x,OJ=y,
∵OJ⊥MN,OM=ON,
∴JM=JN=![]() ,
,
在![]() 中,
中,
![]() ,即
,即![]() ①,
①,
在![]() 中, AO=
中, AO=![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ②,
②,
联立①②并解得![]() ,
,![]() ,
,
∴![]() ,OJ=
,OJ=![]() ,
,
∴S△MON=![]() .
.
如图3﹣2中,连接ON,作NJ⊥AB于J交DE于K.
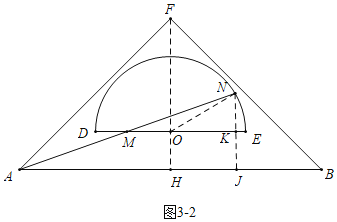
∵AM=MN,MK∥AJ,
∴MK是![]() 的中位线,
的中位线,
∴NK=JK=OH=1,MK=![]() AJ,
AJ,
∵NJ⊥AB,DE∥AB,
∴NK⊥OE,
∴sin∠NOK=![]() ,
,
∵![]() ,
,
∴∠NOK=![]() ,
,
∴OK=![]() NK=
NK=![]() ,
,
∵NJ⊥AB,FH⊥AB,DE∥AB,
∴四边形OKJH是矩形,
∴HJ=OK=![]() ,
,
∴AJ= AH+ HJ =4+![]() ,
,
∴MK=![]() AJ=2+
AJ=2+![]() ,
,
∴OM=MK﹣OK= 2+![]() ﹣
﹣![]() =2﹣
=2﹣![]() ,
,
∴S△MON=![]() (2﹣
(2﹣![]() )×1=1﹣
)×1=1﹣![]() ,
,
综上所述,满足条件的△MON的面积为![]() 或1﹣
或1﹣![]() .
.