题目内容
【题目】已知一次函数y=﹣![]() x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
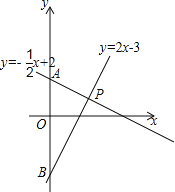
(1)求△PAB的面积;
(2)求证:∠APB=90°;
(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP的面积关于x的函数关系式,并写出相应x的取值范围.
【答案】(1)5;(2)证明见解析;(3)当x>2时,△NAP的面积S=![]() (x﹣2);
(x﹣2);
当x<2时,△NAP的面积S=![]() (2﹣x).
(2﹣x).
【解析】
试题分析:(1)首先解两个一次函数的解析式组成的方程组求得P的坐标,然后求得A和B的坐标,则AB的长即可求得,根据三角形的面积即可求得;
(2)利用勾股定理的逆定理求解;
(3)表示出PN的长,然后根据三角形的面积公式即可求解.
解:(1)根据题意得: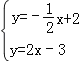 ,
,
解得:![]() ,
,
则P的坐标是(2,1).
在y=﹣![]() x+2中令x=0,解得y=2,则A的坐标是(0,2),
x+2中令x=0,解得y=2,则A的坐标是(0,2),
在y=2x﹣3中令x=0,解得y=﹣3,则B的坐标是(0,﹣3),
则AB=5,
则S△PAB=![]() ×5×2=5;
×5×2=5;
(2)∵PA2=22+(2﹣1)2=5,
BP2=22+(1+3)2=20,
AB2=25,
∴PA2+BP2=AB2,
∴△PAB是直角三角形,∠APB=90°;
(3)N的横坐标是x,则纵坐标是(x,2x﹣3).
则PN=![]() =
=![]() |x﹣2|,
|x﹣2|,
当x>2时,PN=![]() (x﹣2),
(x﹣2),
则△NAP的面积S=![]() PAPN=
PAPN=![]() ×
×![]() ×
×![]() (x﹣2)=
(x﹣2)=![]() (x﹣2);
(x﹣2);
当x<2时,PN=![]() (2﹣x),
(2﹣x),
则△NAP的面积S=![]() PAPN=
PAPN=![]() ×
×![]() ×
×![]() (2﹣x)=
(2﹣x)=![]() (2﹣x).
(2﹣x).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目