题目内容
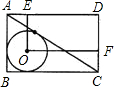
如图,在矩形ABCD中,连接AC,如果O为△ABC的内心,过O作OE⊥AD于E,作OF⊥CD于F,则矩形OFDE的面积与矩形ABCD的面积的比值为( )
A.
| B.
| C.
| D.不能确定 |

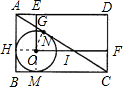
如图,设⊙O交AB于H,交BC于M,交AC于N,
那么OM⊥BC,OH⊥AB,ON⊥AC,
∴四边形AEOH,四边形OMCF均为矩形,四边形BMOH为正方形.
设⊙O的半径为r,那么AE=CF=ON=r,
在△AEG和△OGN中,∠AEG=∠ONG=90°,∠AGE=∠OGN,AE=ON=r,
∴△AEG≌△ONG,
同理△ONI≌△CFI,
∴S△ONG=S△AEG,S△ONI=S△CFI,
S□OEDF=S多边形EGIFD+S△OGI=S多边形EGIFD+S△ONG+S△ONI,
而S多边形EGIFD+S△AEG+S△IFC=S△ADC=
| 1 |
| 2 |
∴S□OEDF=
| 1 |
| 2 |
故选A.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )



 .
. 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( ) DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.