题目内容
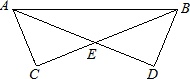 23、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
23、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长.
分析:(1)先证明Rt△ACE≌Rt△BDE,再利用全等三角形的性质可得AE=BE;
(2)再利用等腰直角三角形的性质可以知道CE=AE=1.
(2)再利用等腰直角三角形的性质可以知道CE=AE=1.
解答:解:(1)在Rt△ACE和Rt△BDE中,
∵∠AEC与∠BED是对顶角,∴∠AEC=∠BED. (1分)
∵∠C=∠D=90°,AC=BD.
∴Rt△ACE≌Rt△BDE. (3分)
∴AE=BE. (4分)
(2)∵∠AEC=45°,∠C=90°,
∴∠CAE=45°. (5分)
∴CE=AC=1. (7分)
∵∠AEC与∠BED是对顶角,∴∠AEC=∠BED. (1分)
∵∠C=∠D=90°,AC=BD.
∴Rt△ACE≌Rt△BDE. (3分)
∴AE=BE. (4分)
(2)∵∠AEC=45°,∠C=90°,
∴∠CAE=45°. (5分)
∴CE=AC=1. (7分)
点评:本题利用了三角形全等的判定和性质,以及等腰直角三角形的性质.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
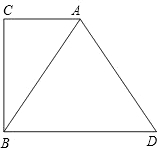 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.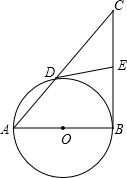 (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.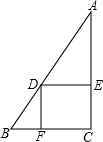 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.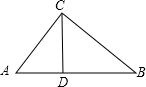 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.