题目内容
已知（-1，y1），（-2，y2），（-4，y3）是抛物线y=-2x2-8x+m上的点，则
- A.y1＜y2＜y3
- B.y3＜y2＜y1
- C.y3＜y1＜y2
- D.y2＜y3＜y1
C
分析：求出抛物线的对称轴，结合开口方向画出草图，根据对称性解答问题．
解答：抛物线y=-2x2-8x+m的对称轴为x=-2，且开口向下，x=-2时取得最大值．
∵-4＜-1，且-4到-2的距离大于-1到-2的距离，根据二次函数的对称性，y3＜y1．
∴y3＜y1＜y2．
∴故选C．
点评：此题考查了二次函数的性质，通常根据开口方向、对称轴，结合草图即可判断函数值的大小．
分析：求出抛物线的对称轴，结合开口方向画出草图，根据对称性解答问题．
解答：抛物线y=-2x2-8x+m的对称轴为x=-2，且开口向下，x=-2时取得最大值．
∵-4＜-1，且-4到-2的距离大于-1到-2的距离，根据二次函数的对称性，y3＜y1．
∴y3＜y1＜y2．
∴故选C．
点评：此题考查了二次函数的性质，通常根据开口方向、对称轴，结合草图即可判断函数值的大小．
练习册系列答案
相关题目
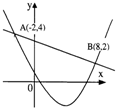11、如图，已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（-2，4），B（8，2），则关于x的不等式ax2+（b-k）x+c-m＞0的解集是