题目内容
已知二次函数y1=ax2+bx+c(a≠0)的图象经过三点(1,0),(-3,0),(0,-| 3 | 2 |

(1)求二次函数的解析式.
(2)在给定的直角坐标系中作出这个函数的图象,并观察图象,写出x为何值,y<0.
分析:(1)由题意知二次函数y1=ax2+bx+c(a≠0)的图象经过两点(1,0),(-3,0),故设抛物线解析式为y=a(x-1)(x+3),然后把点(0,-
)代入即可求出a的值.
(2)首先找到二次函数图象的顶点坐标和对称轴,然后在平面直角坐标系上作出图象.
| 3 |
| 2 |
(2)首先找到二次函数图象的顶点坐标和对称轴,然后在平面直角坐标系上作出图象.
解答: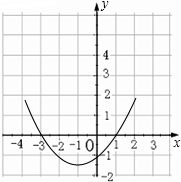 解:(1)设抛物线解析式为y=a(x-1)(x+3),
解:(1)设抛物线解析式为y=a(x-1)(x+3),
将(0,-
)代入,解得a=
.
∴抛物线解析式为y=
x2+x-
,
(2)
由图可以看出当-3<x<1时,y<0.
 解:(1)设抛物线解析式为y=a(x-1)(x+3),
解:(1)设抛物线解析式为y=a(x-1)(x+3),将(0,-
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)
由图可以看出当-3<x<1时,y<0.
点评:本题主要考查用待定系数法求二次函数的解析式和作二次函数的图象的知识点,特别是作图的时候要仔细,作出的图形要美观大方,此题难度一般.

练习册系列答案
相关题目
 已知二次函数y1=x2-2x-1的图象和反比例函数
已知二次函数y1=x2-2x-1的图象和反比例函数 如图,已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(-2,4),B(8,2),则能使y1<y2成立的x的取值范围是
如图,已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(-2,4),B(8,2),则能使y1<y2成立的x的取值范围是 (2013•吴江市模拟)如图,已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于A(-1,2)、B(4,1)两点,则关于x的不等式ax2+bx+c>kx+m的解集是
(2013•吴江市模拟)如图,已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于A(-1,2)、B(4,1)两点,则关于x的不等式ax2+bx+c>kx+m的解集是 已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.
已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.