题目内容
【题目】如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).
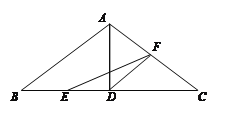
(1)求x为何值时,△EFC和△ACD相似;
(2)是否存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;
(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.
【答案】(1)![]()
(2)不存在.
(3)![]()
【解析】分析:(1)点F在AC上,点E在BD上时,①当![]() 时,△CFE∽△CDA,②当
时,△CFE∽△CDA,②当![]() 时,分别列出方程求解即可;
时,分别列出方程求解即可;
(2)不存在.分两种情形说明:如图2中,当点F在AC上,点E在BD上时,作FH⊥BC于H,EF交AD于N.只要证明EN=FN即可解决问题;
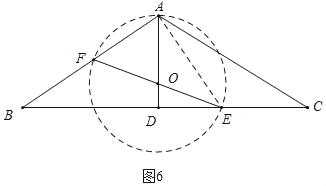
(3)分四种情形①如图3中,当以EF为直径的⊙O经过点A时,⊙O与线段AC有两个交点,连接AE,则∠EAF=90°.②如图4中,当⊙O与AC相切时,满足条件,此时t=![]() .③如图5中,当⊙O与AB相切时,④如图6中,⊙O经过点A时,连接AE,则∠EAF=90°.分别求解即可.
.③如图5中,当⊙O与AB相切时,④如图6中,⊙O经过点A时,连接AE,则∠EAF=90°.分别求解即可.
详解:(1)如图1中,
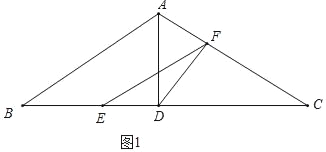
点F在AC上,点E在BD上时,①当![]() 时,△CFE∽△CDA,
时,△CFE∽△CDA,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
②当![]() 时,即
时,即![]() =
=![]() ,
,
∴t=2,
当点F在AB上,点E在CD上时,不存在△EFC和△ACD相似,
综上所述,t=![]() s或2s时,△EFC和△ACD相似.
s或2s时,△EFC和△ACD相似.
(2)不存在.
理由:如图2中,当点F在AC上,点E在BD上时,作FH⊥BC于H,EF交AD于N.
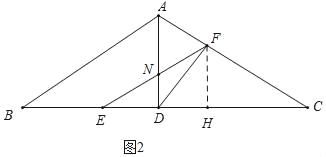
∵CF=5t.BE=4t,
∴CH=CFcosC=4t,
∴BE=CH,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴DE=DH,
∵DN∥FH,
∴![]() =1,
=1,
∴EN=FN,
∴S△END=S△FND,
∴△EFD被 AD分得的两部分面积相等,
同法可证当点F在AB上,点E在CD上时,△EFD被 AD分得的两部分面积相等,
∴不存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5.
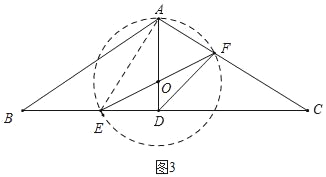
(3)①如图3中,当以EF为直径的⊙O经过点A时,⊙O与线段AC有两个交点,连接AE,则∠EAF=90°.
由![]() =cosC=
=cosC=![]() ,可得
,可得![]() =
=![]() ,
,
∴t=![]() ,
,
∴0≤t<![]() 时,⊙O与线段AC只有一个交点.
时,⊙O与线段AC只有一个交点.
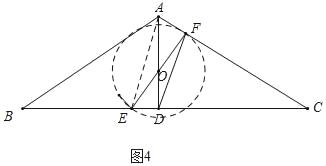
②如图4中,当⊙O与AC相切时,满足条件,此时t=![]() .
.
③如图5中,当⊙O与AB相切时,cosB=![]() ,即
,即![]() =
=![]() ,解得t=
,解得t=![]() .
.
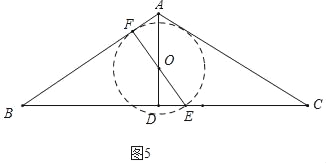
④如图6中,⊙O经过点A时,连接AE,则∠EAF=90°.
由cosB=![]() =
=![]() ,即
,即![]() =
=![]() ,t=
,t=![]() ,
,
∴![]() <t≤4时,⊙O与线段AC只有一个交点.
<t≤4时,⊙O与线段AC只有一个交点.
综上所述,当⊙O与线段AC只有一个交点时,0≤t<![]() 或
或![]() 或
或![]() 或
或![]() <t≤4.
<t≤4.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?