Question

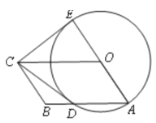
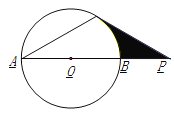
【题目】如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，AC＝CP．

(1) 求证：CP是⊙O的切线；

(2) 若PC＝6,AB=4，求图中阴影部分的面积．

Answer 1

【答案】(1)、证明过程见解析；(2)、6－2π

【解析】

试题分析：(1)、连接OC，根据∠A的度数以及AC=CP得出∠A=∠P=30°，根据OC=OA得出∠COP=60°，从而得到∠OCP的度数；(2)、根据AB的长度得出OC和OB的长度，从而求出扇形OBC的面积，然后利用△PCO的面积减去扇形OBC的面积得到阴影部分的面积.

试题解析：(1)、连结OC ∵∠A=30°，AC=CP ∴∠P=∠A=30° ∵OC=OA

∴∠COP=2∠A=60° ∴∠OCP=90° ∴OC⊥PC ∴PC是⊙O的切线

(2)、∵AB=4 ∴OC=OB=2 ∴S扇OBC=2

S=S△PCO-S扇OBC =6-2